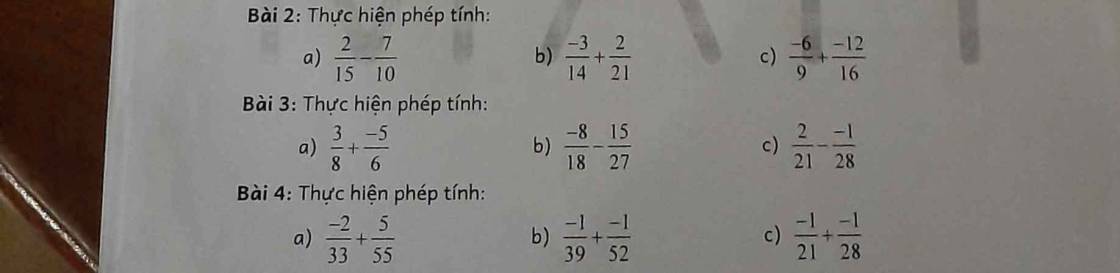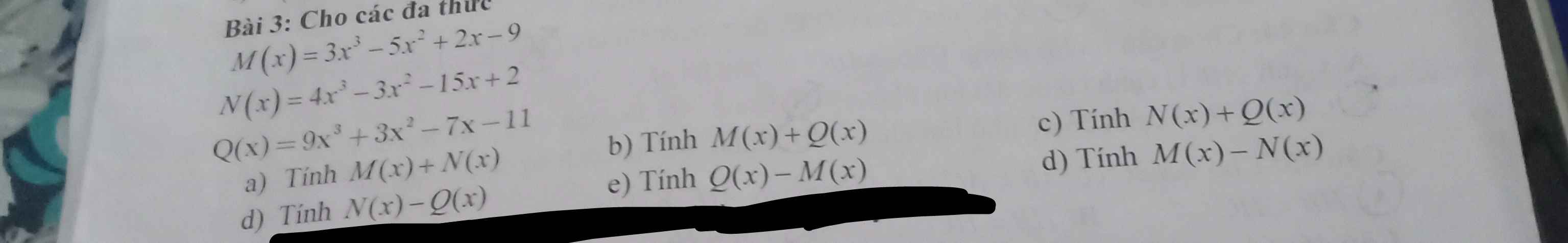Ai giúp tui 2 bài này với

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

❖ミ★𝓣𝓻𝓪𝓷𝓰 (𝓯𝓪𝓷 𝓛𝓝𝓓)★彡『ʈєɑɱ❖๖ۣۜƝƘ☆...

2 tháng 9 2021 - olm

Ai giúp tui 2 bài này với

#Toán lớp 7

❖ミ★𝓣𝓻𝓪𝓷𝓰 (𝓯𝓪𝓷 𝓛𝓝𝓓)★彡『ʈєɑɱ❖๖ۣۜƝƘ☆...

2 tháng 9 2021

Bào 6 và bài 7 nhé

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Quỳnh Trang

6 tháng 7 2023

ai giúp tui 3 đến 2 bài này vs cảm ơn mn nhiều cần gấp ạ

#Toán lớp 7

HT.Phong (9A5)

CTVHS

6 tháng 7 2023

Bài 2:

a) \(\dfrac{2}{15}-\dfrac{7}{10}=\dfrac{4}{30}-\dfrac{21}{30}=-\dfrac{17}{30}\)

b) \(\dfrac{-3}{14}+\dfrac{2}{21}=\dfrac{-9}{42}+\dfrac{4}{42}=\dfrac{-5}{42}\)

c) \(\dfrac{-6}{9}+\dfrac{-12}{16}=\dfrac{-96}{144}+\dfrac{-108}{144}=\dfrac{-204}{144}=-\dfrac{17}{12}\)

Đúng(2)

HT.Phong (9A5)

CTVHS

6 tháng 7 2023

Bài 3:

a) \(\dfrac{3}{8}+\dfrac{-5}{6}=\dfrac{3}{8}-\dfrac{5}{6}=\dfrac{18}{48}-\dfrac{40}{48}=-\dfrac{22}{48}=-\dfrac{11}{24}\)

b) \(\dfrac{-8}{18}-\dfrac{15}{27}=\dfrac{-24}{54}-\dfrac{30}{54}=\dfrac{-54}{54}=-1\)

c) \(\dfrac{2}{21}-\dfrac{-1}{28}=\dfrac{8}{84}-\dfrac{-3}{84}=\dfrac{11}{84}\)

Đúng(0)

Bùi Nguyên Thành Đạt

29 tháng 10 2021

ai giải giúp tui 2 câu này với

#Toán lớp 7

blueesky~~~

29 tháng 10 2021

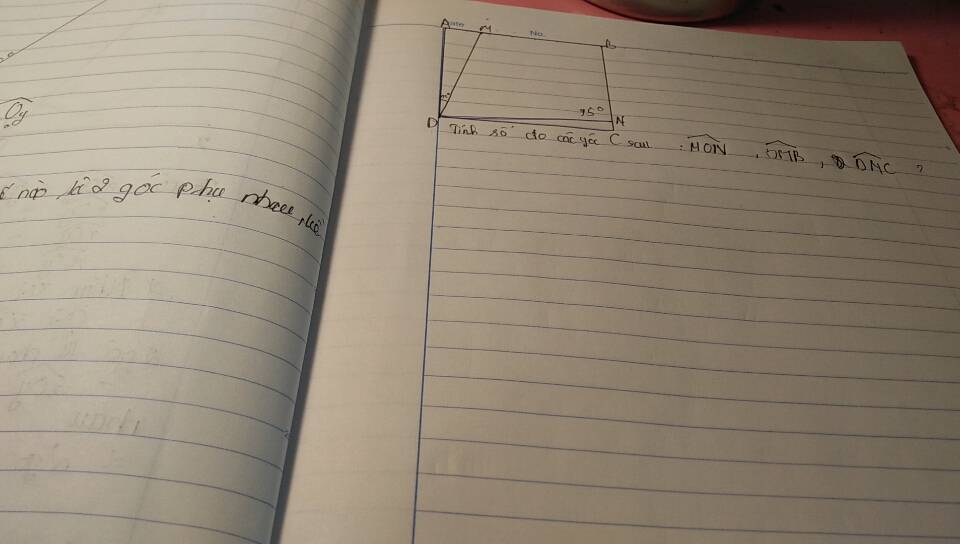
Bài 4:
Ta có: Góc A và góc O là hai trong cùng phía => Ax// Oz (1)
Góc O và góc B là hai góc trong cùng phía => Oz// By (1)
Từ (1 ) và (2 ) => Az// By
Mình chỉ biết vậy thoi, có j sai thì xin lỗi nhaa

Đúng(0)

Bùi Nguyên Thành Đạt

29 tháng 10 2021

Đúng(0)

tran minh tri

9 tháng 4 2017 - olm

ai làm giúp tui bài này thanks nhìu

#Toán lớp 7

Thu Hương

9 tháng 4 2017

bài nào vậy bạn

Đúng(0)

thao nguyen phuong hien

9 tháng 4 2017

bài j z p

Đúng(0)

Longphuoc Lehoang

7 tháng 12 2023

AI GIÚP TUI ĐỀ NÀY VỚI :((

#Toán lớp 7

Nguyễn Lê Phước Thịnh

7 tháng 12 2023

Câu 3:

Gọi số học sinh giỏi của ba lớp 7A,7B,7C lần lượt là a(bạn),b(bạn),c(bạn)

(Điều kiện: \(a,b,c\in Z^+\))

Vì số học sinh giỏi của ba lớp 7A,7B,7C lần lượt tỉ lệ với 4;3;2 nên \(\dfrac{a}{4}=\dfrac{b}{3}=\dfrac{c}{2}\)

Tổng số học sinh giỏi của ba lớp là 108 bạn nên a+b+c=108

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{4}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a+b+c}{4+3+2}=\dfrac{108}{9}=12\)

=>\(a=12\cdot4=48;b=3\cdot12=36;c=2\cdot12=24\)

Vậy: Lớp 7A có 48 bạn học sinh giỏi, lớp 7B có 36 bạn học sinh giỏi, lớp 7C có 24 bạn học sinh giỏi

I: Trắc nghiệm

Câu 1: D

Câu 2: A

Câu 3: B

Câu 4: D

Câu 5: C

Câu 6: A

Câu 7: D

Câu 8: C

Đúng(2)

Thiên Vũ Hàn

30 tháng 10 2021 - olm

Giúp tui giải bài này với mọi người ! Tui cần gấp lắm !

#Toán lớp 7

ᏉươℕᎶ ℕè ²ᵏ⁹

30 tháng 10 2021

Bài nào???

Đúng(0)

49.Trần Ngọc Phương Vy

30 tháng 10 2021

bài nào vậy bạn

Đúng(0)

Trần Thị Diệu

8 tháng 10 2021

Giúp tui với bài 36 tui ko biết làm ai giúp tui được hông sắp hết thời gian rồi 😢😭

#Toán lớp 7

Thị Thư Nguyễn

8 tháng 10 2021

Bài nào vậy bn bn phải nói rõ chứ

Đúng(0)

Trần Thị Diệu

8 tháng 10 2021

hình học, bài 36 tui hông biết làm 😢

Đúng(0)

nguyett anhh

7 tháng 8 2023

giúp tui hai bài này với ạaaa ♡

#Toán lớp 7

Nguyễn Lê Phước Thịnh

7 tháng 8 2023

1: x^3-5x+a chia hết cho x-3

=>x^3-9x+4x-12+a+12 chia hết cho x-3

=>a+12=0

=>a=-12

2: 2x^2+x+a chia hết cho x+3

=>2x^2+6x-5x-15+a+15 chia hết cho x+3

=>a+15=0

=>a=-15

3: x^3+2x^2+a chia hết cho x+3

=>x^3+3x^2-x^2+9+a-9 chia hết cho x+3

=>a-9=0

=>a=9

4: 4x^2-6x+a chia hết cho x-3

=>4x^2-12x+6x-18+a+18 chia hết cho x-3

=>a+18=0

=>a=-18

5: 2x^2+ax-4 chia hết cho x+4

=>2x^2+8x+(a-8)x+4a-32-4a+24 chia hết cho x+4

=>-4a+24=0

=>a=6

6: x^3-7x^2+ax chia hết cho x-2

=>x^3-2x^2-5x^2+10x+(a-10)x-2(a-10)+2(a-10) chia hết cho x-2

=>2(a-10)=0

=>a=10

Đúng(2)

Tieen Ddat dax quay trow lai

7 tháng 8 2023

lm nhanh zữ

Đúng(0)

hoangvietdung

27 tháng 6 2023

bài này làm thế nào mọi người giúp tui với

#Toán lớp 7

Nguyễn Phạm Anh Khoa

18 tháng 3 2017 - olm

Ai giúp hộ tui bài này với ( Vẽ Hình cho tui nữa nha )

Cho tam giác ABC cân tại A. Gọi M là trung điểm của AC. N là trung điểm của AB

Chứng minh BM = CN

Cô tớ nói là có 3 cách làm lận. Giúp tớ nha !!!

#Toán lớp 7

Nguyễn Phạm Anh Khoa

18 tháng 3 2017

Làm 3 cách lun nha

Đúng(0)

Vũ Như Mai

18 tháng 3 2017

Làm tạm 1 cách thôi nhé

Xét \(\Delta BNC\)và \(\Delta BMC\)có:

\(BN=CM\)(Vì tam giác ABC cân tại A => AB = AC => 1/2 AB = 1/2 AC)

\(\widehat{ABC}=\widehat{ACB}\)(Vì tam giác ABC cân tại A)

\(BC\): chung

\(\Rightarrow\Delta BNC=\Delta CMB\left(c.g.c\right)\)

\(\Rightarrow BM=CN\)(2 cạnh t.ứng)

Đúng(0)

Cone Conehead

13 tháng 5 2022

bài này có ai nhờ tui mà tui k biết làm ai đó chỉ dùng tui đi

#Toán lớp 7

Nguyễn Lê Phước Thịnh

14 tháng 6 2023

a: M(x)+N(x)=7x^3-8x^2-13x-7

b: M(x)+Q(x)=12x^3-2x^2-5x-20

c: N(x)+Q(x)=13x^3-22x-9

d: N(x)-Q(x)=-5x^3-6x^2-8x+13

e: Q(x)-M(x)=6x^3+8x^2-9x-2

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP