
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1:
Áp dụng t/c dtsbn:
a) \(\dfrac{x}{7}=\dfrac{y}{4}=\dfrac{x-y}{7-4}=\dfrac{24}{3}=8\)
\(\Rightarrow\left\{{}\begin{matrix}x=8.7=56\\y=8.4=32\end{matrix}\right.\)
b) \(\dfrac{x}{6}=\dfrac{y}{2}=\dfrac{z}{5}=\dfrac{x-y+z}{6-2+5}=\dfrac{18}{9}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.6=12\\y=2.2=4\\z=2.5=10\end{matrix}\right.\)
Bài 2:
Gọi số HS 3 lớp 7A,7B,7C lần lượt là a,b,c(học sinh), \(\left(a,b,c>0\right)\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{7}=\dfrac{a+b+c}{5+6+7}=\dfrac{126}{18}=7\)
\(\Rightarrow\left\{{}\begin{matrix}a=7.5=35\\b=7.6=42\\c=7.7=49\end{matrix}\right.\)



Gọi x,y,z là số học sinh khối 6, 7, 8
(x,y,z>0, đvị là học sinh)
Đã biết khối học sinh lớp 8 ít hơn số hs khối 6 là 120 hs
x-z=120
x, y, z tỉ lệ với 8, 7, 5
x/8=y/7=z/5
Áp dụng tính chất dãy tỉ số bằng nhau có:
x/8=y/7=z/5= x-z/8-5=120/3=40
=> x/8= 40 => x=40.8=320 => số hs khối 6 là 320 hs
y/7= 40 y=40.7= 280 số hs khối 7 là 280 hs
z/5= 40 z=40.5=200 số hs khối 8 là 200 hs

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên AD=AE
=>BE=CD
Xét ΔEIB vuông tại E và ΔDIC vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó: ΔEIB=ΔDIC
c: Ta có: ΔEIB=ΔDIC
nên IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC

a: Xét ΔAMC và ΔEMB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)
MC=MB
Do đó: ΔAMC=ΔEMB
b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE

a, \(2y^2\left(8y^6\right)y=16y^9\)
b, \(=\dfrac{3}{4}x^3y^4\)
c, \(=10x^3y^4z^8\)
d, \(=\left(\dfrac{3}{4}x^2y^3\right)\left(\dfrac{12}{5}x^4\right)=\dfrac{9}{5}x^6y^3\)
e, \(=-\dfrac{5}{4}x^5y^{10}\)
f, \(=120x^4y^6z^4\)

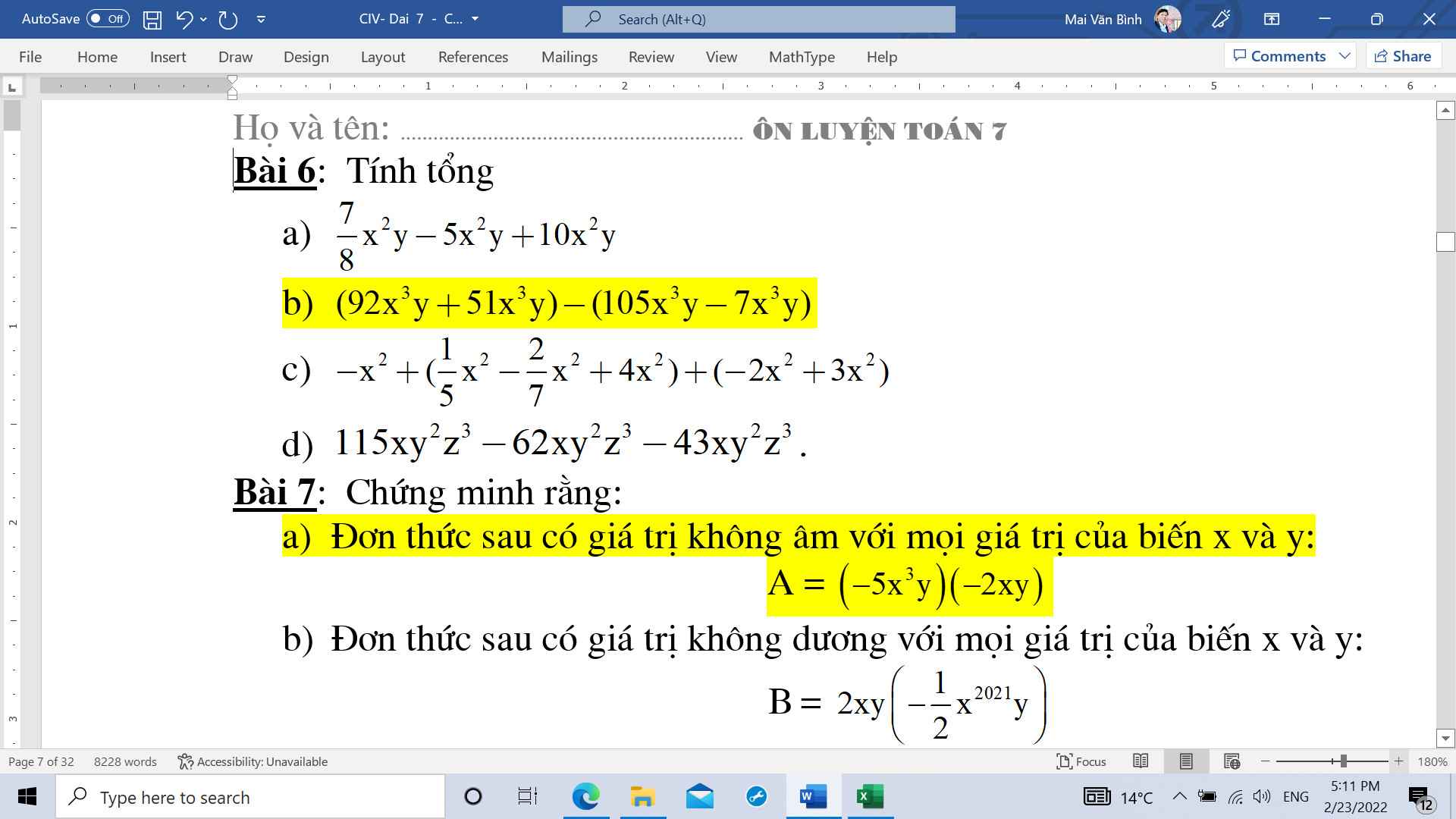



 ai giúp với mình với
ai giúp với mình với giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước


a: Xét ΔADE và ΔCDB có
DA=DC
\(\widehat{ADE}=\widehat{CDB}\)
DE=DB
Do đó: ΔADE=ΔCDB
còn câu b,c nx bạn