ai giúp mình với, tối mình nộp rồi huhu :<<
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 10 2021
\(g,ĐK:x\ge0\\ PT\Leftrightarrow10\sqrt{x}+8\sqrt{x}-11\sqrt{x}=21\\ \Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ h,ĐK:x\ge0\\ PT\Leftrightarrow6\sqrt{3x}+2\sqrt{3x}-3\sqrt{3x}=15\\ \Leftrightarrow\sqrt{3x}=5\Leftrightarrow3x=25\Leftrightarrow x=\dfrac{25}{3}\left(tm\right)\\ i,ĐK:x\ge0\\ PT\Leftrightarrow12\sqrt{x}-21-2\sqrt{x}+10=6\sqrt{x}-12\\ \Leftrightarrow4\sqrt{x}=-1\Leftrightarrow\sqrt{x}=-\dfrac{1}{4}\Leftrightarrow x\in\varnothing\\ j,ĐK:x\ge2\\ PT\Leftrightarrow6\sqrt{x-2}-15\cdot\dfrac{1}{5}\sqrt{x-2}=20+4\sqrt{x-2}\\ \Leftrightarrow\sqrt{x-2}=-20\Leftrightarrow x\in\varnothing\)
\(k,ĐK:x\ge3\\ PT\Leftrightarrow6\sqrt{x-3}-\dfrac{1}{5}\cdot5\sqrt{x-3}-\dfrac{1}{7}\cdot7\sqrt{x-3}=20\\ \Leftrightarrow4\sqrt{x-3}=20\Leftrightarrow\sqrt{x-3}=5\\ \Leftrightarrow x-3=25\Leftrightarrow x=28\left(tm\right)\\ l,ĐK:x\ge5\\ PT\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\\ \Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\\ \Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)
A
0
A
1
10 tháng 11 2021
\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)
A
1
8 tháng 11 2021
8.
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đt luôn đi qua với mọi m
\(\Leftrightarrow mx_0+2y_0-3my_0+m-1=0\\ \Leftrightarrow m\left(x_0-3y_0+1\right)+\left(2y_0-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-3y_0+1=0\\2y_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{2}\\y_0=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Vậy đt luôn đi qua \(A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) với mọi m
9.
PT giao Ox là \(y=0\Leftrightarrow mx+m-1=0\Leftrightarrow x=\dfrac{1-m}{m}\Leftrightarrow A\left(\dfrac{1-m}{m};0\right)\Leftrightarrow OA=\left|\dfrac{1-m}{m}\right|\)
PT giao Oy là \(x=0\Leftrightarrow\left(2-3m\right)y+m-1=0\Leftrightarrow y=\dfrac{1-m}{2-3m}\Leftrightarrow B\left(0;\dfrac{1-m}{2-3m}\right)\Leftrightarrow OB=\left|\dfrac{1-m}{2-3m}\right|\)
Để \(\Delta OAB\) cân thì \(OA=OB\Leftrightarrow\left|\dfrac{1-m}{m}\right|=\left|\dfrac{1-m}{2-3m}\right|\)
\(\Leftrightarrow\left|m\right|=\left|2-3m\right|\Leftrightarrow\left[{}\begin{matrix}m=2-3m\\m=3m-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\) thỏa mãn đề
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
7 tháng 3 2022
\(\left\{{}\begin{matrix}2x+y=1\\x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x+y=-1\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=9\\x-y=-6\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}2x=3\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{15}{2}\end{matrix}\right.\)\(\left\{{}\begin{matrix}2x+3y=6\\x-2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+6y=12\\3x-6y=9\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}7x=21\\3x-6y=9\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
24 tháng 1 2022
a) ĐKXĐ: \(x>0;x\ne\pm1.\)
\(A=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{1-x}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\right).\\ A=\dfrac{x+2\sqrt{x}+1+x-\sqrt{x}-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\)
\(A=\dfrac{2x+1}{4\sqrt{x}}.\)
b) \(A=\dfrac{3}{4}.\Rightarrow\dfrac{2x+1}{4\sqrt{x}}=\dfrac{3}{4}.\Rightarrow12\sqrt{x}-8x+4=0.\\ \Leftrightarrow8x-12\sqrt{x}-4=0.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=\dfrac{3+\sqrt{17}}{4}.\\\sqrt{x}=\dfrac{3-\sqrt{17}}{4}.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{13+3\sqrt{17}}{8}.\\x=\dfrac{13-3\sqrt{17}}{8}.\end{matrix}\right.\) (TM).
26 tháng 6 2023
1:
a: =>(x-1)(x-7)=0
=>x=1 hoặc x=7
b: =>x(x^2-9x+8)=0
=>x(x-1)(x-8)=0
=>\(x\in\left\{0;1;8\right\}\)
c: Đặt 1/căn x-7=a; 1/căn y+6=b
Theo đề, ta có:
7a-4b=5/3 và 5a+3b=13/6
=>a=1/3 và b=1/6
=>x-7=9 và y+6=36
=>x=16 và y=30
Bài 3:
a: Δ=(2m+3)^2-4(m^2+3m+2)
=4m^2+12m+9-4m^2-12m-8=1>0
=>PT luôn có hai nghiệm pb
b: x1^2+x2^2=1
=>(x1+x2)^2-2x1x2=1
=>(2m+3)^2-2(m^2+3m+2)=1
=>4m^2+12m+9-2m^2-6m-4-1=0
=>2m^2+6m+4=0
=>m=-1 hoặc m=-2
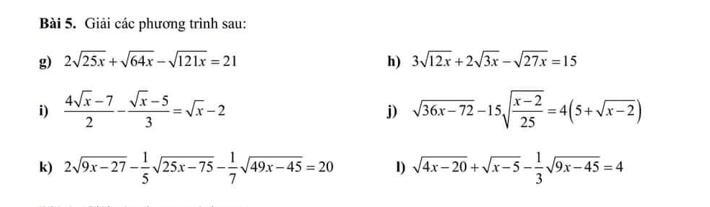
:v câu nào
Câu 15 :
a, \(\left(x-1\right)\left(x+2\right)+2=0\Leftrightarrow x^2+x=0\Leftrightarrow x=-1;x=0\)
b, \(x^2-\left(1+\sqrt{2}\right)x+\sqrt{2}=0\)
\(\Leftrightarrow x^2-x-\sqrt{2}x+\sqrt{2}=0\Leftrightarrow x\left(x-1\right)-\sqrt{2}\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{2}\right)\left(x-1\right)=0\Leftrightarrow x=1;x=\sqrt{2}\)
Bài 16 : Hoành độ giao điểm thỏa mãn pt : \(x^2=2x+3\Leftrightarrow x=3;x=-1\)
TH1 : Thay x = 3 vào y = x^2 => \(y=9\)
TH2 : Thay x = -1 vào y = x^2 => \(y=1\)
Vậy tọa độ probol (P) và (d) là A(3;9) ; B(-1;1)
Em ko chắc :> em nghĩ cách làm giống đồ thị hs thôiii