K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 11 2019
Đặt \(A=\left(x+3\right)\left(x^2-3x+9\right)-\left(54+x^3\right)\)
\(A=x^3+27-54-x^3\)
\(A=27\)
Thay x = 27 vào biểu thức , ta có : A = 27
Vậy........................
NT
3
17 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`(8x-3)(3x+2)-(4x+7)(x+4)=(2x+1)(5x-1)-33`
`\Leftrightarrow 8x(3x+2) -3(3x+2) - 4x(x+4) + 7(x+4) = 2x(5x-1) + 5x-1 - 33`
`\Leftrightarrow 24x^2 + 16x - 9x - 6 - 4x^2 - 16x - 7x - 28 = 10x^2 - 2x + 5x - 1 - 33`
`\Leftrightarrow 20x^2 -16x - 34 = 10x^2 + 3x - 34`
`\Leftrightarrow 20x^2 - 16x - 34 - 10x^2 - 3x + 34 = 0`
`\Leftrightarrow 10x^2 - 19x = 0`
`\Leftrightarrow x(10x - 19)=0`
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\10x-19=0\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\10x=19\end{matrix}\right.\)
`\Leftrightarrow `\(\left[{}\begin{matrix}x=0\\x=\dfrac{19}{10}\end{matrix}\right.\)
Vậy, `x={0; 19/10}.`
AH
Akai Haruma
Giáo viên
29 tháng 1 2023
Lời giải:
$a+b+c=0$
$\Rightarrow a+b=-c$
$\Rightarrow (a+b)^2=(-c)^2$
$\Rightarrow a^2+b^2-c^2=-2ab$
$\Rightarrow \frac{ab}{a^2+b^2-c^2}=\frac{ab}{-2ab}=\frac{-1}{2}$
Tương tự với các phân thức còn lại suy ra:
$A=\frac{-1}{2}+\frac{-1}{2}+\frac{-1}{2}=\frac{-3}{2}$
31 tháng 8 2021
b: Xét ΔBID có \(\widehat{DBI}=\widehat{DIB}\left(=\widehat{IBC}\right)\)
nên ΔBID cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\left(=\widehat{ICB}\right)\)
nên ΔEIC cân tại E
c: Ta có: DE=DI+IE
mà DI=DB
và EC=IE
nên DE=DB+EC
18 tháng 8 2017
dap an ra \(\left(x-3+\sqrt{6}\right).\left(x-3-\sqrt{6}\right)\)
LT
1
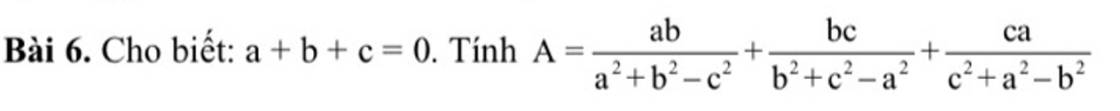
nếu bn đưa = bao nhiêu mới giải đc