BN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 12 2018
\(y'=\left(m^2-2\right)cosx-\dfrac{1}{cos^2x}\)
Để hàm số nghịch biến trên \(\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\Rightarrow y'\le0\) \(\forall x\in\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
Đặt \(cosx=t\Rightarrow0< t\le1\) \(\forall x\in\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
\(y'=\left(m^2-2\right)t-\dfrac{1}{t^2}\le0\) \(\Leftrightarrow m^2-2\le\dfrac{1}{t^3}\Leftrightarrow m^2\le\dfrac{1}{t^3}+2\) \(\forall t\in\text{(0;1]}\)
Đặt \(f\left(t\right)=\dfrac{1}{t^3}+2\Rightarrow m^2\le\min\limits_{\text{(0;1]}}f\left(t\right)\)
\(f'\left(t\right)=-\dfrac{3}{t^4}< 0\) \(\forall t\in\text{(0;1]}\) \(\Rightarrow f\left(t\right)\) nghịch biến \(\Rightarrow\min\limits_{\text{(0;1]}}f\left(t\right)=f\left(1\right)=3\)
\(\Rightarrow m^2\le3\Rightarrow-\sqrt{3}\le m\le\sqrt{3}\) \(\Rightarrow m=\left\{-1;0;1\right\}\)
\(\Rightarrow\) có 3 giá trị nguyên của m để hàm số nghịch biến trên \(\left(\dfrac{-\pi}{2};\dfrac{\pi}{2}\right)\)
2 tháng 4 2019
đáp án là :
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔ 
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
2 tháng 4 2019
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
P/S : quá dễ , t là thần đồng mà .
Mỗi ngày 3 T i c k , giờ làm như lời hứa đi
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2019
Đặt \(cotx=t\Rightarrow\) khi x chạy từ \(\dfrac{\pi}{4}\rightarrow\dfrac{\pi}{2}\) thì \(t\) chạy từ 1 về 0
Do đó, nếu \(f\left(x\right)\) đồng biến thì \(f\left(t\right)=\dfrac{2t+1}{t+m}\) nghịch biến trên \(\left(0;1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}2m-1< 0\\\left[{}\begin{matrix}-m< 0\\-m>1\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{2}\\\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}0< m< \dfrac{1}{2}\\m< -1\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2019
Hàm \(f\left(t\right)\) là hàm bậc nhất trên bậc nhất nên nó nghịch biến khi ad-bc<0
Hơn nữa, 1 điều cần rất chú ý trong loại toán tìm khoảng (a;b) nghịch biến cho hàm bậc nhất trên bậc nhất là là nghiệm của phương trình "mẫu thức = 0" cần né khoảng này ra. Ví dụ, để hàm \(f\left(t\right)\) đồng biến trên (0;1) thì trước hết nó phải liên tục, ko bị gián đoạn trên đoạn này
Mà pt mẫu \(t+m=0\) có nghiệm \(t=-m\)
Nên \(-m\) phải nằm ngoài khoảng \(\left(0;1\right)\) tức \(-m< 0\) hoặc \(-m>1\)
Bạn hiểu chưa ạ?
AM
10 tháng 9 2020
Đặt t=cotx, t>0
Ta có: y=\(\frac{t+1}{10t+m}\)
\(\Rightarrow y'=\frac{m-10}{\left(10t+m\right)^2}\)
Để hàm số đồng biến trên \(\left(0;\frac{\pi}{2}\right)\)mà hàm số t lại nghịch biến trên \(\left(0;\frac{\pi}{2}\right)\)thì m-10<0
\(\Leftrightarrow m< 10\)
Lại có điều kiện để hàm số xác định: 10t+m\(\ne0\) \(\Leftrightarrow10t\ne-m\)\(\Leftrightarrow-10t\ne m\)
Mà t>0 \(\Rightarrow-10t< 0\:\Rightarrow m\ge0\)
Vậy \(0\le m< 10\) thì hàm số đồng biến trên \(\left(0;\frac{\pi}{2}\right)\)
Không hiểu thì bạn hỏi lại mình nha ><
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2020
Đặt \(cotx=t\) \(\Rightarrow t>0\)
Ta thấy rằng khi x tăng trên \(\left(0;\frac{\pi}{2}\right)\) thì t giảm trên \(\left(0;+\infty\right)\)
Do đó hàm \(y=\frac{cotx+1}{10cotx+m}\) tăng trên \(\left(0;\frac{\pi}{2}\right)\Leftrightarrow y=\frac{t+1}{10t+m}\) giảm trên \(\left(0;+\infty\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y'=\frac{m-10}{\left(10t+m\right)^2}< 0\\-\frac{m}{10}\notin\left(0;+\infty\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 10\\-\frac{m}{10}\le0\end{matrix}\right.\) \(\Leftrightarrow0\le m< 10\)
CM
4 tháng 8 2017
y’ = 2x ≤ 0 trên đoạn [-3; 0]. Vậy hàm số nghịch biến trên đoạn [-3,0].
Khi đó trên đoạn [-3,0]: hàm số đạt giá trị lớn nhất tại x = -3 và giá trị lớn nhất bằng 9, hàm số đạt giá trị nhỏ nhất tại x = 0 và giá trị nhỏ nhất = 0.
PT
1
CM
20 tháng 7 2017
y = x – sinx, x ∈ [0; 2 π ].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2 π ]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2 π .
Vậy hàm số đồng biến trên đoạn [0; 2 π ].
P
2
21 tháng 6 2021
kiểu bài này có đáp án trên mạng rồi ấy ạ, anh/chị/ bạn nào mà xem qua đáp án trên mạng có thể giải thích kĩ hơn giúp em chỗ cos 1/x >0 về đoạn sau được không ạ, chứ ai đọc mãi mà không hiểu được 😭😭
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
Bất phương trình lượng giác:
\(cos\left(X\right)\ge a\Leftrightarrow-arccos\left(a\right)+k2\pi\le X\le arccos\left(a\right)+k2\pi\)
Vậy BPT: \(cos\left(\dfrac{1}{x}\right)>0\)
\(\Leftrightarrow-\dfrac{\pi}{2}+k2\pi\le\dfrac{1}{x}\le\dfrac{\pi}{2}+k2\pi\) với \(k\ge1\)
Nghịch đảo: \(\dfrac{2}{k4\pi-\pi}\le x\le\dfrac{2}{k4\pi+\pi}\)
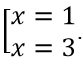
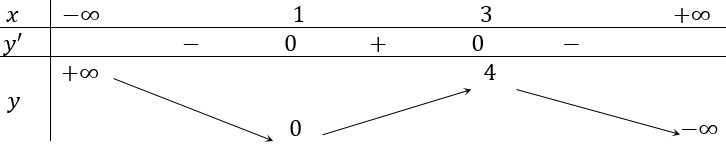
Lời giải:
Ta có: \(y'=\frac{1}{\cos ^2x}-\frac{1}{\sin ^2x}=\frac{\sin ^2x-\cos^2x}{\sin ^2x\cos^2x}=\frac{1-2\cos^2x}{\sin ^2x\cos^2x}\)
Với \(x\in \left(0,\frac{\pi}{2}\right)\) ta chia làm hai đoạn:
+) \(x\in \left(0,\frac{\pi}{4}\right] \Rightarrow 1-2\cos^2x\leq 0\), hàm là hàm nghịch biến
+) \(x\in \left[\frac{\pi}{4},\frac{\pi}{2}\right)\Rightarrow 1-2\cos^2x\geq 0\), hàm là hàm đồng biến