Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^
.
.
hoặc 
.
.
Chọn B
Đặt 
, 
thì 
.
Ta có:
.
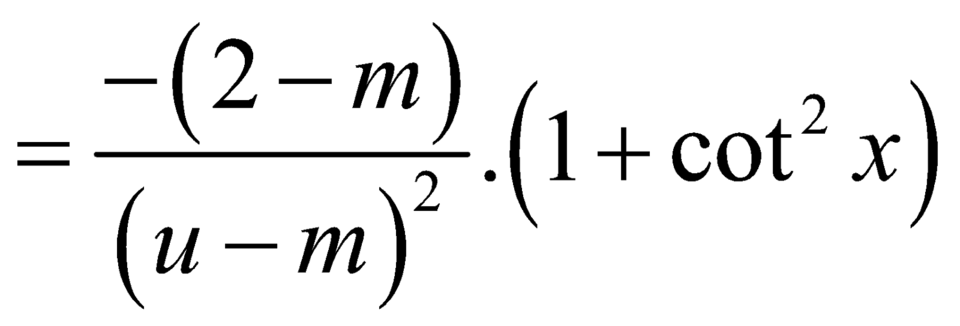Hàm số đồng biến trên 
với mọi 
thuộc 
hay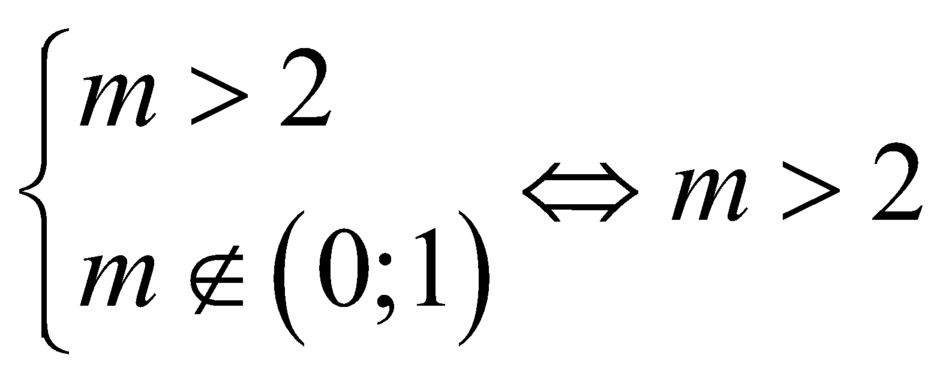 
.
.
.
.
.
\(f'\left(x\right)=m^2x^4-mx^2+20x-\left(m^2-m-20\right)\)
Để hàm số đồng biến trên \(ℝ\)thì \(f'\left(x\right)\ge0,\)với mọi \(x\inℝ\).
Mà ta thấy \(f'\left(-1\right)=m^2-m-20-\left(m^2-m-20\right)=0\)
do đó \(x=-1\)là một điểm cực trị của hàm số \(f'\left(x\right)\).
Ta có: \(f''\left(x\right)=4m^2x^3-2mx+20\)
\(f''\left(-1\right)=0\Leftrightarrow-4m^2+2m+20=0\Leftrightarrow\orbr{\begin{cases}m=\frac{5}{2}\\m=-2\end{cases}}\).
Thử lại.
Với \(m=\frac{5}{2}\): \(f''\left(x\right)=25x^3-5x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\)
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Với \(m=-2\): \(f''\left(x\right)=16x^3+4x+20\)
\(f''\left(x\right)=0\Leftrightarrow x=-1\).
\(f'\left(-1\right)=0\)
do đó \(f'\left(x\right)\ge0\)thỏa mãn.
Vậy tổng các giá trị của \(m\)là: \(\frac{5}{2}+\left(-2\right)=\frac{1}{2}\).
Chọn D.
Xét
\(y'=4x^3-4\left(m-1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=m-1\end{cases}}\)
TH1:
\(m-1\le0\) thì hàm số đồng biến trên R
TH2: \(m-1>0\Rightarrow\orbr{\begin{cases}x=\sqrt{m-1}\\x=-\sqrt{m-1}\end{cases}}\)
Khi đó khoảng đồng biến của hàm số là \(\left(-\infty,-\sqrt{m-1}\right)\text{ và }\left(0,\sqrt{m-1}\right)\)
Muốn hàm số đồng biến trên (1,3) thì \(\left(1,3\right)\subset\left(0,\sqrt{m-1}\right)\Leftrightarrow3\le\sqrt{m-1}\Leftrightarrow m\ge10\)
Vậy \(\orbr{\begin{cases}m\le1\\m\ge10\end{cases}}\)
.
.
.
.
Chọn B
Vì trên 
thì 
nhận tất cả các giá trị thuộc khoảng 
nên hàm số xác trên 
khi 
. Ta có 
.
. Vậy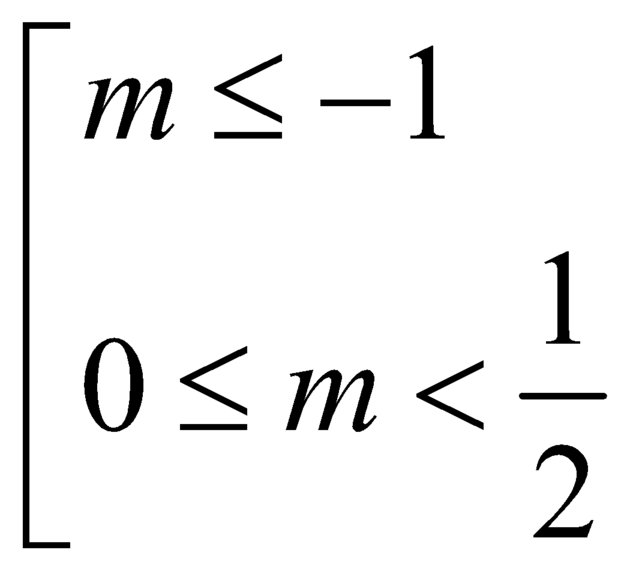 
.
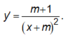
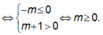
Đặt t=cotx, t>0
Ta có: y=\(\frac{t+1}{10t+m}\)
\(\Rightarrow y'=\frac{m-10}{\left(10t+m\right)^2}\)
Để hàm số đồng biến trên \(\left(0;\frac{\pi}{2}\right)\)mà hàm số t lại nghịch biến trên \(\left(0;\frac{\pi}{2}\right)\)thì m-10<0
\(\Leftrightarrow m< 10\)
Lại có điều kiện để hàm số xác định: 10t+m\(\ne0\) \(\Leftrightarrow10t\ne-m\)\(\Leftrightarrow-10t\ne m\)
Mà t>0 \(\Rightarrow-10t< 0\:\Rightarrow m\ge0\)
Vậy \(0\le m< 10\) thì hàm số đồng biến trên \(\left(0;\frac{\pi}{2}\right)\)
Không hiểu thì bạn hỏi lại mình nha ><
Đặt \(cotx=t\) \(\Rightarrow t>0\)
Ta thấy rằng khi x tăng trên \(\left(0;\frac{\pi}{2}\right)\) thì t giảm trên \(\left(0;+\infty\right)\)
Do đó hàm \(y=\frac{cotx+1}{10cotx+m}\) tăng trên \(\left(0;\frac{\pi}{2}\right)\Leftrightarrow y=\frac{t+1}{10t+m}\) giảm trên \(\left(0;+\infty\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y'=\frac{m-10}{\left(10t+m\right)^2}< 0\\-\frac{m}{10}\notin\left(0;+\infty\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 10\\-\frac{m}{10}\le0\end{matrix}\right.\) \(\Leftrightarrow0\le m< 10\)