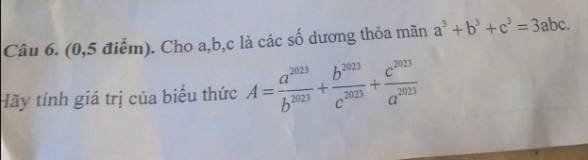K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
0
TH
1
29 tháng 12 2023
\(a^3+b^3+c^3=3abc\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(a^2+b^2+c^2-ab-ac-bc=0\)
=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
=>\(\left(a^2-2ba+b^2\right)+\left(b^2-2cb+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
\(A=\dfrac{a^{2023}}{b^{2023}}+\dfrac{b^{2023}}{c^{2023}}+\dfrac{c^{2023}}{a^{2023}}\)
\(=\dfrac{a^{2023}}{a^{2023}}+\dfrac{b^{2023}}{b^{2023}}+\dfrac{c^{2023}}{c^{2023}}\)
=1+1+1
=3
4 tháng 9 2021
a)
\(16x^2-\left(4x-5\right)^2=15\)
\(\left(4x-4x+5\right)\left(4x+4x-5\right)=15\)
\(5\left(8x-5\right)=15\)
40x-25=15
40x=40
x=1
4 tháng 9 2021
b: Ta có: \(\left(2x+3\right)^2-4\left(x-1\right)\left(x+1\right)=49\)
\(\Leftrightarrow4x^2+12x+9-4x^2+16=49\)
\(\Leftrightarrow12x=24\)
hay x=2
d: Ta có: \(2\left(x+1\right)^2-\left(x-3\right)\left(x+3\right)-\left(x-4\right)^2=0\)
\(\Leftrightarrow2x^2+4x+2-x^2+9-x^2+8x-16=0\)
\(\Leftrightarrow12x=5\)
hay \(x=\dfrac{5}{12}\)
29 tháng 12 2021
b: \(\Leftrightarrow\left(x-3\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=5\end{matrix}\right.\)
24 tháng 10 2021
\(x^2-x-6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}A=3^4+2\cdot3^3+2\cdot3^2+2\cdot3+1=160\\A=\left(-2\right)^4+2\cdot\left(-2\right)^3+2\cdot\left(-2\right)^2+2\cdot\left(-2\right)+1=5\end{matrix}\right.\)
MM
Mai Minh Tú
VIP
7 tháng 1 2022
9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999911111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111112222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222233333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444445555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555566666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888101010101010101010010101010100101010101001001010101010100101010101001010101010100101010101010010101010011001
10 tháng 11 2021
a) Áp dụng Pi-ta-go ta có:
\(AB^2+AC^2=BC^2\Rightarrow AB=\sqrt{20^2-16^2}\Rightarrow AB=18\)
Vì CD=DB, CE=CA⇒DE là đường trung bình trong tam giác ABC
\(\Rightarrow DE=\dfrac{1}{2}AB=\dfrac{1}{2}.18=9\)
10 tháng 11 2021
b) DE là đường trung bình trong tam giác ABC⇒DE//AB mà AB⊥AC⇒DE⊥AC
Vì AF=FB, CD=DB⇒DF là đường trung bình trong tam giác ABC⇒DF//AC mà AC⊥AB, DF⊥AB
Xét tứ giác AEDF có \(\widehat{DEF}=\widehat{AFD}=\widehat{EAF}\) \(\Rightarrow\)AEDF là hình chữ nhật
⇒AD=EF, ED=AF=FB
Ta có: DF⊥AB, AF=FB⇒DF là trung trực của AB⇒AD=DB=EF
Xét tứ giác EDBF có: ED=BF, EF=DB⇒EDBF là hình bình hành
5 tháng 1 2022
a: \(A=\dfrac{2x^2+x^2-1-2x^2+2x+1}{x\left(x+1\right)}=\dfrac{x^2+2x}{x\left(x+1\right)}=\dfrac{x+2}{x+1}\)
b: Ta có: \(x^2-2x=0\)
=>x=2
Thay x=2 vào A, ta được:
\(A=\dfrac{2+2}{2+1}=\dfrac{4}{3}\)
DT
5 tháng 1 2022
(a)
\(A=\dfrac{2x}{x+1}+\dfrac{x-1}{x}-\dfrac{2x^2-2x-1}{x^2+x}\\ =\dfrac{2x}{x+1}+\dfrac{x-1}{x}-\dfrac{2x^2-2x-1}{x\left(x+1\right)}=\dfrac{2x^2}{x\left(x+1\right)}+\dfrac{x^2-1}{x\left(x+1\right)}-\dfrac{2x^2-2x-1}{x\left(x-1\right)}\)
\(=\dfrac{2x^2+x^2-1-2x^2+2x+1}{x\left(x+1\right)}=\dfrac{x^2+2x+1}{x\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+1\right)}{x\left(x+1\right)}=\dfrac{x+1}{x}\)
(b)
\(x^2-2x=0\\ x\left(x-2\right)=0\)
=>x=0 hoặc x=2 mà đk x khác 0 nên thay x=2 vào bt A , ta có:
\(\dfrac{x+1}{x}=\dfrac{2+1}{2}=\dfrac{3}{2}\)
