
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Rightarrow P=\left(\dfrac{\left(y-x\right)\left(y+x\right)}{y-x}-\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(x-y\right)\left(x+y\right)}\right).\dfrac{x+y}{y^2-2xy+x^2+xy}\)
\(\Rightarrow P=\left(y+x-\dfrac{x^2+xy+y^2}{x+y}\right).\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{\left(x+y\right)^2-\left(x^2+xy+y^2\right)}{x+y}.\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{x^2+2xy+y^2-x^2-xy-y^2}{x+y}.\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{xy}{x+y}.\dfrac{x+y}{y^2-xy+x^2}\)
\(\Rightarrow P=\dfrac{xy}{y^2-xy+x^2}\)

Bài 4:
a) Ta có: AM+MB=AB
AN+NC=AC
mà MB=NC
và AB=AC
nên AM=AN
Xét ΔABC có
\(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
nên MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
b) Ta có: ΔABC cân tại A
nên \(\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}=\dfrac{180^0-40^0}{2}=70^0\)
\(\Leftrightarrow\widehat{BMN}=\widehat{CNM}=180^0-70^0=110^0\)
Bài 3:
Ta có: ABCD là hình thang cân
nên AD=BC
mà AD=AB
nên BC=AB
Xét ΔBAC có BA=BC(cmt)
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)(hai góc ở đáy)
mà \(\widehat{BAC}=\widehat{ACD}\)(hai góc so le trong, AB//CD
nên \(\widehat{BCA}=\widehat{DCA}\)
hay CA là tia phân giác của \(\widehat{BCD}\)

a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)

9, = \(\left(x^2\right)^2-\left(\dfrac{2}{5}y\right)^2=x^4-\dfrac{4}{25}y^2\)
10, = \(\left(\dfrac{x}{2}\right)^2-y^2=\dfrac{x^2}{4}-y^2\)

\(a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)=5^3-3.1.5=110\)

a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC

11.\(=\left(\dfrac{x}{2}\right)^2-2.\dfrac{x}{2}.2y+\left(2y\right)^2\)
12. \(=\sqrt{2x}^2-2.\sqrt{2x}.y+y^2\)
13. \(=\left(\dfrac{3}{2}x\right)^2+2.\dfrac{3}{2}x.3y+\left(3y\right)^2\)
14.\(=\sqrt{2x}^2+2.\sqrt{2x}.\sqrt{8y}+\sqrt{8y}^2\)
(tự làm nữa nhá. cứ áp dụng cái công thức là ra mà.
Công thức sgk trang 16 nhá)

\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
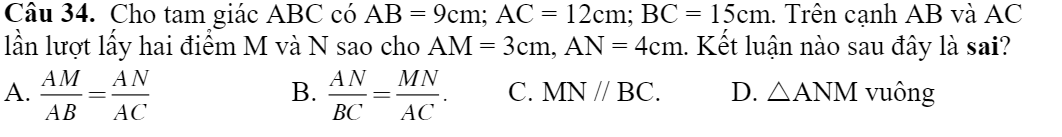



 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ