
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)

\(d,=\dfrac{3y}{5x\left(x-y\right)}\\ e,=\dfrac{5x\left(x+2\right)\left(2-x\right)}{4\left(x-2\right)\left(x+2\right)}=\dfrac{-5x}{4}\\ f,=\dfrac{3\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)\left(6-x\right)}=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\\ g,=\dfrac{3xy\left(x-3y\right)\left(x+3y\right)}{2x^2y^2\left(x-3y\right)}=\dfrac{3\left(x+3y\right)}{2xy}\\ h,=\dfrac{45x^2y\left(x-y\right)\left(x+y\right)}{10xy\left(y-x\right)}=\dfrac{-9x\left(x+y\right)}{2}\\ i,=\dfrac{12\left(a-b\right)\left(a+b\right)\left(a^2+ab+b^2\right)}{3\left(a+b\right)\left(a-b\right)^2}=\dfrac{4\left(a^2+ab+b^2\right)}{a-b}\)
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)



6) \(\left(2x+\dfrac{1}{2}\right)^3=8x^3+4x^2+\dfrac{3}{2}x+\dfrac{1}{8}\)
7) \(\left(x-3\right)^3=x^3-9x^2+27x-27\)

Câu 19:
\(=\dfrac{11x+x-18}{2x-3}=\dfrac{12x-18}{2x-3}=6\)
Câu 20:
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5\left(x-5\right)}\)
\(=\dfrac{15x+25+x^2-25x}{5x\left(x-5\right)}=\dfrac{\left(x-5\right)^2}{5x\left(x-5\right)}=\dfrac{x-5}{5x}\)

a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

Bài 2:
a: =>(x+5)(4-x)=0
=>x=4 hoặc x=-5
b: =>2x(2x-1)=0
=>x=0 hoặc x=1/2
c: =>2x(x^2+1)+x^2+1=0
=>(x^2+1)(2x+1)=0
=>2x+1=0
=>x=-1/2
d: Δ=(-3)^2-4*1*4=9-16=-7<0
=>PTVN

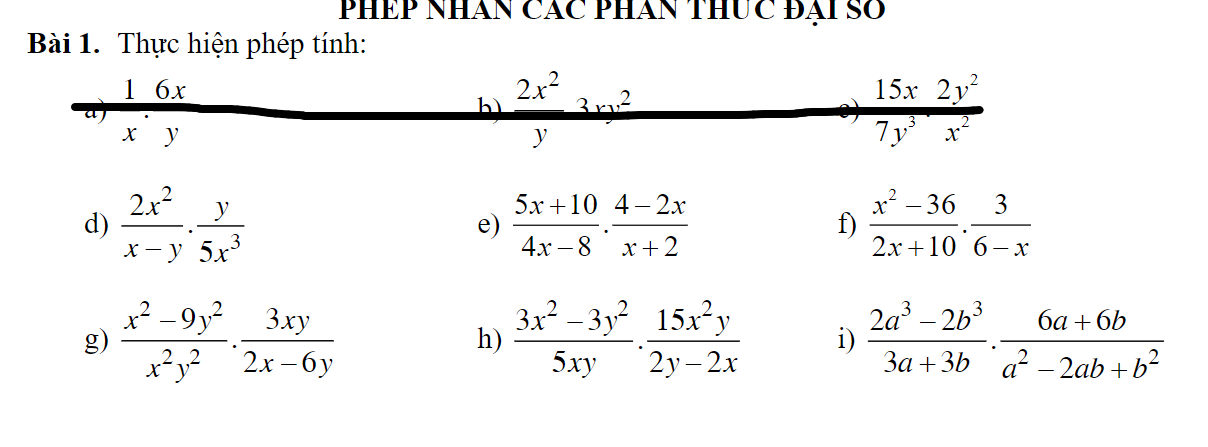

 ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái





4. \(13x^2+8-20xy+25y^2-2x-10y\)
\(=9x^2-6x+1+4x^2+25y^2+1-20xy+4x-10y+6\)
\(=\left(3x-1\right)^2+\left(2x-5y+1\right)^2+6\ge6\)
Dấu \(=\)khi \(\hept{\begin{cases}3x-1=0\\2x-5y+1=0\end{cases}}\Leftrightarrow x=y=\frac{1}{3}\).