
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: \(x^2-6x-y^2-4y+5\)
\(=x^2-6x+9-\left(y^2+4y+4\right)\)
\(=\left(x-3\right)^2-\left(y+2\right)^2\)
b: \(4a^2-12a-b^2+2b+8\)
\(=4a^2-12a+9-\left(b^2-2b+1\right)\)
\(=\left(2a-3\right)^2-\left(b-1\right)^2\)
c: \(\left(x+y-3\right)\left(x+y+3\right)\)
\(=\left(x+y\right)^2-3^2\)
d: \(\left(3z+x+2y\right)\left(2y-x+3z\right)\)
\(=\left(2y+3z\right)^2-x^2\)

(3-12x)(x-1)+(12x-8)(x+2)+x2=52
3(x-1)-12x(x-1)+12x(x+2)-8(x+2)+x2=52
3x-3-12x2+12+12x2+24x-8x-16+x2=52
(3x+24x-8x)+(12-3-16)+(12x2-12x2+x2)=52
19x-7+x2=52
x(19-x)=52+7=59
mà 59 là số ng tố nên x rỗng
Vậy x E \(\theta\)

\(6x^2+xy-7x-2y^2+7y-5=-\left(y-2x-1\right)\left(2y+3x-5\right)\)
\(6x^2+xy-7x-2y^2+7y-5=-2y\left(y-2x-1\right)-3x\left(y-2x-1\right)+5\left(y-2x-1\right)=-\left(y-2x-1\right)\left(2y+3x-5\right)\)

\(2x^2-x.\left(x-2\right)-3=0\)
\(2x^2-x^2+2x-3=0\)
\(x^2+2x-3=0\)
\(\left(x^2-x\right)+\left(3x-3\right)=0\)
\(x.\left(x-1\right)+3.\left(x-1\right)=0\)
\(\left(x-1\right)\left(x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\x+3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-3\end{cases}}}\)
Vậy \(\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)
2x2 - x.( x - 2 ) - 3 = 0
\(\Leftrightarrow2x^2-x^2+2x-3=0\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Leftrightarrow x^2-x+3x-3=0\)
\(\Leftrightarrow x\left(x-1\right)+3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+3=0\\x-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-3\\x=1\end{cases}}\)
Vậy....


5: \(\left(\dfrac{2}{3}x^2-\dfrac{1}{2}y\right)^3=\dfrac{8}{27}x^6-\dfrac{2}{3}x^4y+\dfrac{1}{2}x^2y^2-\dfrac{1}{8}y^3\)

6) \(\left(2x+\dfrac{1}{2}\right)^3=8x^3+4x^2+\dfrac{3}{2}x+\dfrac{1}{8}\)
7) \(\left(x-3\right)^3=x^3-9x^2+27x-27\)

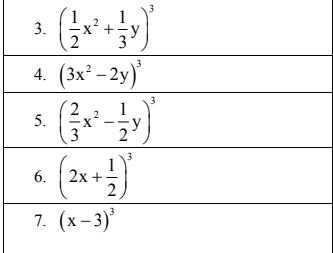 Ai giúp e 5 câu nay` đc không ạ ! e cmơn trước ạ :)))
Ai giúp e 5 câu nay` đc không ạ ! e cmơn trước ạ :))) ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
Tìm X
\(x^3-8+\left(x-2\right)\left(2x+1\right)=0\\ \Rightarrow\left(x-2\right)\left(x^2+x+1\right)+\left(x-2\right)\left(2x+1\right)=0\\ \Rightarrow\left(x-2\right)\left(x^2+x+1+2x+1\right)=0\)
\(\left(x-2\right)\left(x^2+3x+2\right)=0\\ \Rightarrow\left(x-2\right)\left(x+1\right)\left(x+2\right)=0\\ \Rightarrow\hept{\begin{cases}x=-1\\x=2\\x=-2\end{cases}}\)
HT