Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn gõ baohiemnhandao.violympic.vn thì sẽ có đề thi thử của tất cả các lớp và các vòng ở viôlympic và bạn sẽ được thi như thi thật vậy
k mình nhé


Áp dụng định lý Pitago vào tam giác đó ta có:
\(13^2=a^2+b^2\)(1)
\(\frac{1}{2}ab=14=>ab=28\)(2)
Từ 1 và 2 => \(a^2+2ab+b^2=169+56=225\)
Nên áp dụng hđt ta có : \(\left(a+b\right)^2=225\\ a+b=15\)
Ta co Sabc=1/2ab hay 14 =1/2ab suy ra ab=28
Theo dinh ly pytago ta co a^2+b^2=13^2 hay (a+b)^2-2ab=13^22
Ban thay so vao tinh tiep nhe mijh ko mag may tinh

Kham khảo đề tự luận này nè bọn mình thi chúng đấy
Câu 1 (2,0 điểm) Thực hiện phép tính:
a) 2xy.3x2y3
b) x.(x2 - 2x + 5)
c) (3x2 - 6x) : 3x
d) (x2 – 2x + 1) : (x – 1)
Câu 2 (2,0 điểm). Phân tích các đa thức sau thành nhân tử:
a) 5x2y - 10xy2
b) 3(x + 3) – x2 + 9
c) x2 – y2 + xz - yz
Câu 3 (2,0 điểm). Cho biểu thức:
a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định?
b) Rút gọn biểu thức A.
c) Tìm giá trị của biểu thức A tại x = 1.
Câu 4 (3,5 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA.
Câu 5 (0,5 điểm). Cho a + b = 1. Tính giá trị của các biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
Tham khảo nek :
Bài 1: (3 điểm) Giải phương trình và bất phương trình:
C) x – 2)2 + 2(x – 1) ≤ x2 + 4
Bài 2: (2 điểm) Một ô tô đi từ A đến B với vận tốc 60km/h và đi từ B về A với vận tốc 45km/h. Thời gian cả đi và về hết 7 giờ. Tính quãng đường AB.
Bài 3: (1 điểm)Chứng minh rằng nếu a + b = 1 thì a2 + b2 ≥ 1/2
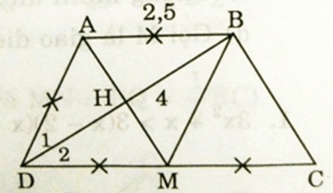
Bài 4: (4 điểm) Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
Đáp án và Hướng dẫn giải
Bài 1
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Bài 2
Gọi x (km) là quãng đường AB (x > 0)
Thời gian đi từ A đến B là: x/60 (giờ)
Thời gian đi từ B về A là: x/45 (giờ)
Theo đề ra, ta có phương trình:
⇔ 3x + 4x = 7.180 ⇔ 7x = 7.180 ⇔ x = 180 (nhận)
Trả lời: Quãng đường AB dài 180km.
Bài 3
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
Bài 4
a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
Xét tam giác vuông AHB, ta có :
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
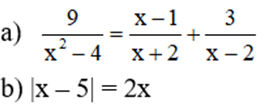
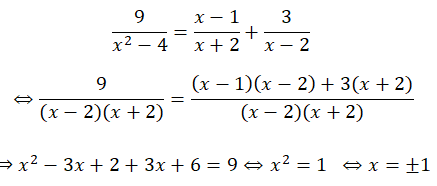
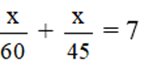
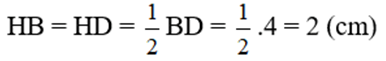
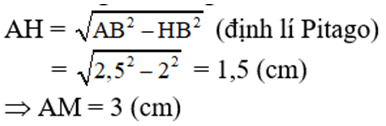
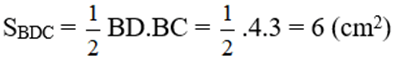
trungcap6
mk 123456789