Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

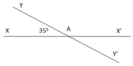
a) Vẽ góc x A y ^ = 35 0
b) Vẽ góc x’Ay’ đối đỉnh với góc xAy
c) x A y ^ = x ' A y ' ^ = 35 0
d) x A y ' ^ = x ' A y ^ = 145 0

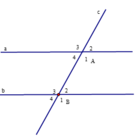
+) Vì a // b nên A ^ 1 + B ^ 2 = 180 ∘ (cặp góc trong cùng phía)
Mặt khác A ^ 1 − B ^ 2 = 70 0
⇒ A ^ 1 = 180 ∘ + 70 ∘ : 2 = 125 ∘ và B ^ 2 = 180 ∘ − 125 ∘ = 55 ∘
+) Ta có A ^ 3 = A ^ 1 (hai góc đối đỉnh) mà A ^ 1 = 125 ∘
⇒ A ^ 3 = 125 ∘
Ta có B ^ 2 = B ^ 4 (hai góc đối đỉnh) mà B ^ 2 = 55 ∘
⇒ B ^ 4 = 55 ∘

Bài 1
a. (Tự vẽ hình)
Áp dụng định lí Py-ta-go, ta có:
BC2= AB2 + AC2
<=> BC2= 62 + 82
<=> BC2= 100
=> BC = 10 (cm)
Bài 1
b. Áp dụng định lí Py-ta-go, ta có:
AC2 = AH2 + HC2
<=> 82 = 4,82 + HC2
<=> 64 = 23,04 + HC2
=> HC2 = 64 - 23,04
=> HC2 = 40,96
=> HC = 6,4 (cm)
=> HB = BC - HC = 10 - 6,4 = 3,6 (cm)

1/ Ta có hình vẽ:
x O y A B C D I Xét tam giác OAD và tam giác OBD có:
O: góc chung
OA = OC (GT)
OB = OD (GT)
=> tam giác OAD = tam giác OBD (c.g.c)
=> BC = AD (2 cạnh tương ứng)
Vậy BC = AD (đpcm)
2/ Ta có hình vẽ:
A B C M D
Mình quên kí hiệu AB = AC rồi, bạn tự bổ sung thêm nhé
a/ Xét tam giác ABM và tam giác DCM có:
AM = MD (GT)
BM = MC (GT)
\(\widehat{AMB}\)=\(\widehat{CMD}\) (đối đỉnh)
=> tam giác ABM = tam giác DCM (c.g.c)
b/ Ta có: tam giác ABM = tam giác DCM (câu a)
=> \(\widehat{ABM}\)=\(\widehat{MCD}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
nên AB//CD (đpcm)
c/ Xét tam giác ABM và tam giác ACM có:
AM: cạnh chung
BM = MC (GT)
AB = AC (GT)
=> tam giác ABM = tam giác ACM (c.c.c)
=> \(\widehat{AMB}\)=\(\widehat{AMC}\) (2 góc tương ứng)
Mà \(\widehat{AMB}\) + \(\widehat{AMC}\) = 1800 (kề bù)
=> \(\widehat{AMB}\) = \(\widehat{AMC}\) = 900
Vậy AM \(\perp\)BC (đpcm)

A B C E D I 1 2 1 2
a) Vì ΔABC cân tại A(gt)
=>\(\widehat{ABC}=A\widehat{CB}\)
Mà: BD, CE là tia phân giác của \(\widehat{ABC};\widehat{ACB}\)
=> \(\widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}\)
=> \(\widehat{B_2}+\widehat{C_2}=\widehat{B_2}+\widehat{B_1}=\widehat{ABC}\)
Xét ΔABC cân tại A(gt)
=> \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-80}{2}=50^o\)
Xét ΔBIC có: \(\widehat{BIC}=180^o-\left(\widehat{B_2}+\widehat{C_2}\right)=180^o-\widehat{ABC}=180-50=130^o\)
b) Xét ΔBIC có: \(\widehat{B_2}=\widehat{C_2}\left(cmt\right)\)
=> ΔBIC cân tại I

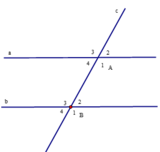
a) Vì B 2 ^ , A 1 ^ là cặp góc trong cùng phía nên ta có:
B 2 ^ + A 1 ^ = 180 0 ⇒ A 1 ^ = 180 0 − B 2 ^ = 180 0 − 45 0 = 135 0 .
b) Ta có B ^ 1 = A ^ 1 = 135 ∘ (hai góc đồng vị)
mà A ^ 3 = A ^ 1 = 135 ∘ (hai góc đối đỉnh)
Vậy B ^ 1 = A ^ 3 = 135 ∘
c) Ta có A ^ 1 + A ^ 2 = 180 ∘ (hai góc kề bù) mà B ^ 1 = A ^ 1 (theo câu b)
Do đó A ^ 2 + B ^ 1 = 180 ∘