Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1
Đặt \(A=a^3+b^3+c^3-3(a-1)(b-1)(c-1)\)
Biến đổi:
\(A=a^3+b^3+c^3-3[abc-(ab+bc+ac)+a+b+c-1]=a^3+b^3+c^3-3abc+3(ab+bc+ac)-6\)
\(A=(a+b+c)^3-3[(a+b)(b+c)(c+a)+abc]-6+3(ab+bc+ac)\)
\(A=21-3(a+b+c)(ab+bc+ac)+3(ab+bc+ac)=21-6(ab+bc+ac)\)
Áp dụng BĐT Am-Gm:
\(3(ab+bc+ac)\leq (a+b+c)^2=9\Rightarrow ab+bc+ac\leq 3\)
\(\Rightarrow A\geq 21-6.3=3\). Dấu bằng xảy ra khi $a=b=c=1$
Vì \(0\leq a,b,c\leq2\Rightarrow (a-2)(b-2)(c-2)\leq 0\)
\(\Leftrightarrow abc-2(ab+bc+ac)+4\leq 0\Leftrightarrow 2(ab+bc+ac)\geq 4+abc\geq 0\Rightarrow ab+bc+ac\geq 2\)
\(\Rightarrow A\leq 21-6.2=9\). Dấu bằng xảy ra khi $(a,b,c)=(0,1,2)$ và các hoán vị.
Bài 2a)
Ta có
\(A=a^2+b^2+c^2=(a+1)^2+(b+1)^2+(c+1)^2-3-2(a+b+c)\)
\(\Leftrightarrow A=(a+b+c+3)^2-2[(a+1)(b+1)+(b+1)(c+1)+(c+1)(a+1)]-3\)
\(\Leftrightarrow A=6-2[(a+1)(b+1)+(b+1)(c+1)+(c+1)(a+1)]\)
Vì \(-1\leq a,b,c\leq 2\Rightarrow a+1,b+1,c+1\geq 0\)
\(\Rightarrow (a+1)(b+1)+(b+1)(c+1)+(c+1)(a+1)\geq 0\Rightarrow A\leq 6\)
Dấu bằng xảy ra khi \((a,b,c)=(-1,-1,2)\) và các hoán vị của nó

Ta có : \(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\le\dfrac{a^3+b^3+c^3}{2abc}+3\)
\(\Leftrightarrow\dfrac{a^2+b^2+c^2}{a^2+b^2}+\dfrac{a^2+b^2+c^2}{b^2+c^2}+\dfrac{a^2+b^2+c^2}{c^2+a^2}\le\dfrac{a^3}{2abc}+\dfrac{b^3}{2abc}+\dfrac{b^3}{2abc}+3\)( vì \(a^2+b^2+c^2=1\) )
\(\Leftrightarrow3+\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2ab}+3\)
\(\Leftrightarrow\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
Mà theo bất đẳng thức cô-si , ta có : \(b^2+c^2\ge2bc\)\(\Rightarrow\dfrac{a^2}{b^2+c^2}\le\dfrac{a^2}{2bc}\)
Tương tự ta cũng có : \(\dfrac{b^2}{c^2+a^2}\le\dfrac{b^2}{2ca},\dfrac{c^2}{a^2+b^2}\le\dfrac{c^2}{2ab}\)
Cộng các bất đẳng thức trên lại với nhau ta được :
\(\Leftrightarrow\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}\le\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
Do đó bất đẳng thức ban đầu được chứng minh .

Theo BĐT tam giác ta có:
\(b+c>a\Rightarrow a+b+c>2a\Rightarrow2>2a\Rightarrow a< 1\)
Tương tự cũng có: \(b<1;c<1\)
Áp dụng BĐT AM-GM ta có:
\(\left(1-a\right)\left(1-b\right)\left(1-c\right)\le\left(\dfrac{1-a+1-b+1-c}{3}\right)^3=\left(\dfrac{3-\left(a+b+c\right)}{3}\right)^3=\dfrac{1}{27}\)
\(\Rightarrow0< \left(1-a\right)\left(1-b\right)\left(1-c\right)\le\dfrac{1}{27}\)
\(\Rightarrow0< ab+bc+ca-abc-\left(a+b+c\right)+1\le\dfrac{1}{27}\)
\(\Rightarrow0< ab+bc+ca-abc-1\le\dfrac{1}{27}\)
\(\Rightarrow1< ab+bc+ca-abc\le\dfrac{28}{27}\)
\(\Rightarrow2< 2ab+2bc+2ca+a^2+b^2+c^2-\left(a^2+b^2+c^2+2abc\right)\le\dfrac{56}{27}\)
\(\Rightarrow2< \left(a+b+c\right)^2-\left(a^2+b^2+c^2+2abc\right)\le\dfrac{56}{27}\)
\(\Rightarrow2< 4-\left(a^2+b^2+c^2+2abc\right)\le\dfrac{56}{27}\)
\(\Rightarrow\dfrac{52}{27}\le a^2+b^2+c^2+2abc< 2\) *Đúng*

\(a+b+c=0\Rightarrow b+c=-a\)
\(\Rightarrow\left(b+c\right)^2=a^2\) \(\Rightarrow b^2+c^2+2bc=a^2\)
\(\Rightarrow a^2-b^2-c^2=2bc\)
Tương tự: \(b^2-c^2-a^2=2ca\) ; \(c^2-a^2-b^2=2ab\)
Mặt khác ta có:
\(a+b+c=0\Rightarrow a+b=-c\Rightarrow\left(a+b\right)^3=-c^3\)
\(\Rightarrow a^3+b^3+3ab\left(a+b\right)=-c^3\)
\(\Rightarrow a^3+b^3+c^3=-3ab\left(a+b\right)=-3ab\left(-c\right)=3abc\)
Đặt vế trái biểu thức cần chứng minh là P
\(\Rightarrow P=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2ab}=\dfrac{a^3+b^3+c^3}{2abc}=\dfrac{3abc}{2abc}=\dfrac{3}{2}\) (đpcm)

\(VT=\dfrac{1}{a^2+bc}+\dfrac{1}{b^2+ac}+\dfrac{1}{c^2+ab}\le\dfrac{1}{2a\sqrt{bc}}+\dfrac{1}{2b\sqrt{ac}}+\dfrac{1}{2c\sqrt{ab}}\)
\(VT\le\dfrac{\sqrt{ab}+\sqrt{ac}+\sqrt{bc}}{2abc}\)
Mặt khác ta luôn có:
\(\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{a}-\sqrt{c}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2\ge0\)
\(\Rightarrow2\left(a+b+c\right)-2\left(\sqrt{ab}+\sqrt{ac}+\sqrt{bc}\right)\ge0\)
\(\Rightarrow\sqrt{ab}+\sqrt{ac}+\sqrt{bc}\le a+b+c\)
\(\Rightarrow VT\le\dfrac{a+b+c}{2abc}\)
Dấu "=" khi \(a=b=c\)

a: \(\Leftrightarrow\dfrac{\left(b+c\right)^3-a^3-3bc\left(b+c\right)}{b+c-a}=a^2\)
\(\Leftrightarrow a^2=\left(b+c\right)^2+a\left(b+c\right)+a^2-\dfrac{3bc\left(b+c\right)}{b+c-a}\)
\(\Leftrightarrow\left(b+c\right)^2+a\left(b+c\right)-\dfrac{3bc\left(b+c\right)}{b+c-a}=0\)
\(\Leftrightarrow\left(b+c\right)\left(b+c-\dfrac{3bc}{b+c-a}+a\right)=0\)
\(\Leftrightarrow\left(b+c\right)\left(b+c-a\right)-3bc+a\left(b+c-a\right)=0\)
\(\Leftrightarrow b^2+2bc+c^2-ab-ac-3bc+ab+ac-a^2=0\)
\(\Leftrightarrow b^2+c^2-a^2-bc=0\)
\(\Leftrightarrow a^2=b^2+c^2-bc\)
\(cosA=\dfrac{b^2+c^2-a^2}{2\cdot b\cdot c}=\dfrac{1}{2}\)
nên góc A=30 độ
b: \(cosB=\dfrac{\left(a+b\right)\left(b+c-a\right)\left(c+a-b\right)}{2bac}\)
=>\(\dfrac{\left(a+b\right)\left[c-\left(a-b\right)\right]\left[c+\left(a-b\right)\right]}{2abc}=\dfrac{a^2+c^2-b^2}{2ac}\)
\(\Leftrightarrow\dfrac{\left(a+b\right)\cdot\left[c^2-\left(a-b\right)^2\right]}{b}=a^2+c^2-b^2\)
\(\Leftrightarrow c^2\left(a+b\right)-\left(a+b\right)\left(a-b\right)^2=a^2b+c^2b-b^3\)
\(\Leftrightarrow ac^2+bc^2-\left(a^2-b^2\right)\left(a-b\right)=a^2b+c^2b-b^3\)
\(\Leftrightarrow ac^2+bc^2-a^3+a^2b+ab^2-b^3=a^2b+c^2b-b^3\)
\(\Leftrightarrow ac^2+bc^2-a^3+ab^2=c^2b\)
\(\Leftrightarrow ac^2+bc^2-a^3-ab^2-c^2b=0\)
\(\Leftrightarrow c^2\left(a+b\right)-a\left(a^2+b^2\right)-c^2b=0\)
=>c^2*a-a(a^2+b^2)=0
=>a(c^2-a^2-b^2)=0
=>c^2=a^2+b^2
=>góc A=90 độ

Lời giải:
Áp dụng BĐT AM-GM cho các số dương:
\(a^2+bc\geq 2\sqrt{a^2bc}; b^2+ac\geq 2\sqrt{b^2ac}; c^2+ab\geq 2\sqrt{c^2ab}\)
Do đó:
\(\text{VT}=\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{1}{2\sqrt{a^2bc}}+\frac{1}{2\sqrt{b^2ac}}+\frac{1}{2\sqrt{c^2ab}}\)
hay \(\text{VT}\leq \frac{\sqrt{bc}+\sqrt{ac}+\sqrt{ab}}{2abc}(*)\)
Tiếp tục áp dụng BĐT AM-GM:
\(\left\{\begin{matrix} \sqrt{bc}\leq \frac{b+c}{2}\\ \sqrt{ac}\leq \frac{a+c}{2}\\ \sqrt{ab}\leq \frac{a+b}{2}\end{matrix}\right.\Rightarrow \sqrt{ab}+\sqrt{bc}+\sqrt{ac}\leq a+b+c(**)\)
Từ \((*);(**)\Rightarrow \text{VT}\leq \frac{a+b+c}{2abc}\)
Ta có đpcm
Dấu bằng xảy ra khi \(a=b=c\)

3/ Áp dụng bất đẳng thức AM-GM, ta có :
\(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}\ge2\sqrt{\dfrac{\left(ab\right)^2}{\left(bc\right)^2}}=\dfrac{2a}{c}\)
\(\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge2\sqrt{\dfrac{\left(bc\right)^2}{\left(ac\right)^2}}=\dfrac{2b}{a}\)
\(\dfrac{c^2}{a^2}+\dfrac{a^2}{b^2}\ge2\sqrt{\dfrac{\left(ac\right)^2}{\left(ab\right)^2}}=\dfrac{2c}{b}\)
Cộng 3 vế của BĐT trên ta có :
\(2\left(\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\right)\ge2\left(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\right)\)
\(\Leftrightarrow\dfrac{a^2}{b^2}+\dfrac{b^2}{c^2}+\dfrac{c^2}{a^2}\ge\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}\left(\text{đpcm}\right)\)
Bài 1:
Áp dụng BĐT AM-GM ta có:
\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{1}{2\sqrt{a^2.bc}}+\frac{1}{2\sqrt{b^2.ac}}+\frac{1}{2\sqrt{c^2.ab}}=\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}{2abc}\)
Tiếp tục áp dụng BĐT AM-GM:
\(\sqrt{bc}+\sqrt{ac}+\sqrt{ab}\leq \frac{b+c}{2}+\frac{c+a}{2}+\frac{a+b}{2}=a+b+c\)
Do đó:
\(\frac{1}{a^2+bc}+\frac{1}{b^2+ac}+\frac{1}{c^2+ab}\leq \frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2abc}\leq \frac{a+b+c}{2abc}\) (đpcm)
Dấu "=" xảy ra khi $a=b=c$

1.
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có 2 số cùng phía so với \(\dfrac{2}{3}\), không mất tính tổng quát, giả sử đó là b và c
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\ge0\)
Mặt khác \(0\le a\le1\Rightarrow1-a\ge0\)
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\left(1-a\right)\ge0\)
\(\Leftrightarrow-abc\ge\dfrac{4a}{9}+\dfrac{2b}{3}+\dfrac{2c}{3}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}\)
\(\Leftrightarrow-abc\ge-\dfrac{2a}{9}+\dfrac{2}{3}\left(a+b+c\right)-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}=-\dfrac{2a}{9}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc+\dfrac{8}{9}\)
\(\Leftrightarrow-2abc\ge-\dfrac{4a}{9}-\dfrac{4ab}{3}-\dfrac{4ac}{3}-2bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{ab}{3}-\dfrac{ac}{3}-bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(b+c\right)-bc+\dfrac{16}{9}\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(2-a\right)-\dfrac{\left(b+c\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}+\dfrac{a^2}{3}-\dfrac{2a}{3}-\dfrac{\left(2-a\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge\dfrac{a^2}{12}-\dfrac{a}{9}+\dfrac{7}{9}=\dfrac{1}{12}\left(a-\dfrac{2}{3}\right)^2+\dfrac{20}{27}\ge\dfrac{20}{27}\)
\(\Rightarrow ab+bc+ca\ge2abc+\dfrac{20}{27}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{2}{3}\)


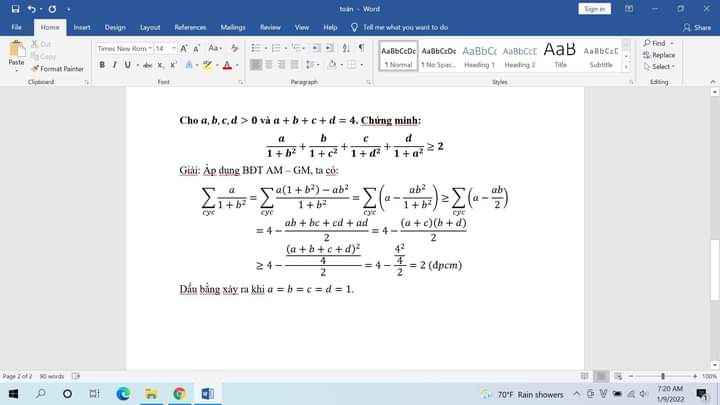
Chả liên quan đến câu hỏi .-.
Viết lộn òi, thông cảm :''(