K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
Đường tròn (C) tâm \(I\left(-2;-2\right)\) bán kính \(R=5\)
Gọi đường thẳng d qua A có dạng: \(a\left(x-6\right)+b\left(y-17\right)=0\)
\(\Leftrightarrow ax+by-6a-17b=0\) (\(a^2+b^2\ne0\))
d là tiếp tuyến của (C) khi và chỉ khi \(d\left(I;d\right)=R\)
\(\Leftrightarrow\dfrac{\left|-2a-2b-6a-17b\right|}{\sqrt{a^2+b^2}}=5\)
\(\Leftrightarrow\left|8a+19b\right|=5\sqrt{a^2+b^2}\)
\(\Leftrightarrow\left(8a+9b\right)^2=25\left(a^2+b^2\right)\)
\(\Leftrightarrow\left(3a+4b\right)\left(13a+84b\right)=0\)
Chọn \(\left(a;b\right)=\left(4;-3\right);\left(84;-13\right)\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}4\left(x-6\right)-3\left(y-17\right)=0\\84\left(x-6\right)-13\left(y-17\right)=0\end{matrix}\right.\) \(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=3\)
\(S_{IAB}=\dfrac{1}{2}IA.IB.sin\widehat{AIB}=\dfrac{1}{2}R^2.sin\widehat{AIB}\le\dfrac{1}{2}R^2\)
\(S_{max}\) khi \(sin\widehat{AIB}=1\Rightarrow\Delta AIB\) vuông cân tại I
\(\Rightarrow AB=R\sqrt{2}=3\sqrt{2}\)
\(\Rightarrow d\left(I;AB\right)=\dfrac{AB}{2}=\dfrac{3\sqrt{2}}{2}\)
Gọi phương trình AB có dạng: \(a\left(x+1\right)+b\left(y+3\right)=0\) với a;b ko đồng thời bằng 0
\(d\left(I;AB\right)=\dfrac{\left|a-2b+a+3b\right|}{\sqrt{a^2+b^2}}=\dfrac{3\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}\left|2a+b\right|=3\sqrt{a^2+b^2}\)
\(\Leftrightarrow2\left(4a^2+4ab+b^2\right)=9\left(a^2+b^2\right)\)
\(\Leftrightarrow a^2-8ab+7b^2=0\Rightarrow\left[{}\begin{matrix}a=b\\a=7b\end{matrix}\right.\)
Chọn b=1 \(\Rightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(1;1\right)\\\left(a;b\right)=\left(1;7\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}1\left(x+1\right)+1\left(y+3\right)=0\\1\left(x+1\right)+7\left(y+3\right)=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
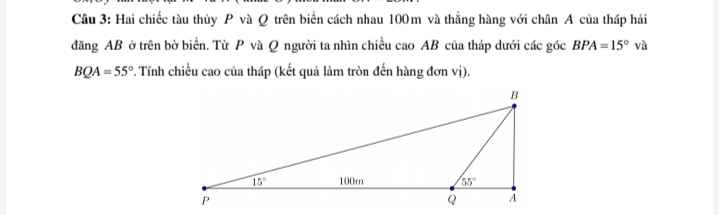
Trong tam giác vuông ABP:
\(tanP=\dfrac{AB}{AP}\Rightarrow AP=\dfrac{AB}{tanP}\Rightarrow PQ+AQ=\dfrac{AB}{tanP}\) (1)
Trong tam giác vuông ABQ:
\(tanQ=\dfrac{AB}{AQ}\Rightarrow AQ=\dfrac{AB}{tanQ}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow PQ+\dfrac{AB}{tanQ}=\dfrac{AB}{tanP}\Rightarrow PQ=AB\left(\dfrac{1}{tanP}-\dfrac{1}{tanQ}\right)\)
\(\Rightarrow AB=\dfrac{PQ}{\dfrac{1}{tanP}-\dfrac{1}{tanQ}}=\dfrac{100}{\dfrac{1}{tan15^0}-\dfrac{1}{tan55^0}}\approx33\left(m\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(A=4\left[\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)\right]-6\left[\left(sin^2a+cos^2a\right)^2-2sin^2a.cos^2a\right]\)
\(=4\left(1-3sin^2a.cos^2a\right)-6\left(1-2sin^2a.cos^2a\right)\)
\(=4-12sin^2a.cos^2a-6+12sin^2a.cos^2a\)
\(=-2\)
30 tháng 6 2023
37:
\(AB=\sqrt{\left(-2-1\right)^2+\left(4-2\right)^2}=\sqrt{13}\)
\(AC=\sqrt{\left(3-1\right)^2+\left(5-2\right)^2}=\sqrt{13}\)
\(BC=\sqrt{\left(3+2\right)^2+\left(5-4\right)^2}=\sqrt{26}\)
Vì AB^2+AC^2=BC^2 và AB=AC
nên ΔABC vuông cân tại A
=>S ABC=1/2*AB*AC=1/2*13=13/2
AH=13/2*2:căn 26=13/căn 26=1/2*căn 26
a+b
=b+a
học
tốt
a+b=b+a=a+b+0=0+b+a