
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.ĐKXĐ \(\hept{\begin{cases}x\ne-3\\x\ne2\end{cases}}\)
A=\(\frac{x+2}{x+3}-\frac{5}{\left(x+3\right)\left(x-2\right)}-\frac{1}{x-2}\)
=\(\frac{\left(x+2\right)\left(x-2\right)-5-\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\frac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}=\frac{\left(x-4\right)\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
=\(\frac{x-4}{x-2}\)
b. Để A >0 thì \(\frac{x-4}{x-2}\) >0 \(\Rightarrow\orbr{\begin{cases}x< 2\\x>4\end{cases}}\)
Kết hợp ĐK thì \(\orbr{\begin{cases}x< 2,x\ne-3\\x>4\end{cases}}\)
c. \(A=\frac{x-4}{x-2}=1+\frac{-2}{x-2}\)
Để A nguyên thì \(x-2\inƯ\left(-2\right)=\left\{-2;-1;1;2\right\}\)
\(\Rightarrow x\in\left\{0,1,3,4\right\}\)
Khi thay vào A, để A dương thì \(x\in\left\{0;1\right\}\)
Vậy để A nguyên dương thì \(x\in\left\{0;1\right\}\)
Câu c, có thể nói kết hợp với điều kiện giải được trong câu b, ta tìm được \(x\in\left\{0;1\right\}\)

Có: \(A=x^3-x^2+2\)
\(=x^3+1-x^2+1\)
\(=\left(x+1\right)\left(x^2-x+1\right)-\left(x+1\right)\left(x-1\right)\)
\(=\left(x+1\right)\left(x^2-2x+2\right)\)
A là số dương
<=> \(\left(x+1\right)\left(x^2-2x+2\right)>0\)
Vì \(x^2-2x+2=\left(x-1\right)^2+1>0\)
=> \(\left(x+1\right)>0\)
<=> x > - 1
A là số nguyên => x nguyên
Vậy để A là số nguyên dương thì x là số nguyên và x > -1.

MK ko biế đúng ko nữa , sai thì ý kiến
a)
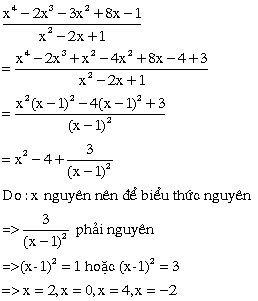
b)
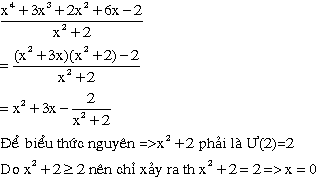
Chúc các bn hok tốt
Tham khảo nhé
Để A là số nguyên dương thì \(x-3\in\left\{1;-1;2;-2;3;6\right\}\)
hay \(x\in\left\{4;2;5;1;6;9\right\}\)