Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

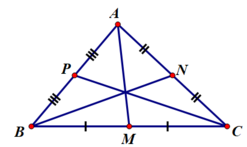
Ta vẽ ΔABC và 3 đường trung tuyến AM, BN, CP
Trong đó : M, N, P lần lượt là trung điểm BC, AC, AB

MN^2 + MP^2 = 6^2 + 8^2 = 100
NP^2 = 10^2 = 100
=> MN^2 + MP^2 = NP^2
TAm giác MNP có MN^2 + MP^2 = NP^2 => tam giác MNP vuông tại P
CÓ MD là trung tuyến => MD = 1/2 NP = 1/2 . 10 = 5
Smnd = 1/2 . MN.MP = 1/2MK . NP
<=> MN . MP = MK . NP => 6.8 = 10 . MK => MK = 6.8 : 10 = 4,8

A B C D E G N M P F
Gọi AM, BN, CP là các đường trung tuyến của ∆ABC cắt nhau tại G.
AG = GD (gt)
AG = 2GM (suy ra từ tính chất đường trung tuyến)
Nên GD = 2GM
GD = GM + MD
=> GM = MD
Xét ∆BMD và ∆CMG:
BM = CM (gt)
\(\widehat{BND}=\widehat{CMG}\left(\text{đối đỉnh}\right)\)
MD = GM (chứng minh trên)
Do đó: ∆BMD = ∆CMG (c.g.c)
=> BD = CG
\(CG=\frac{2}{3}CP\left(\text{tính chất đường trung tuyến}\right)\)
\(\Rightarrow BD=\frac{2}{3}CP\) (1)
\(BG=\frac{2}{3}BN\left(\text{tính chất đường trung tuyến}\right)\) (2)
\(AG=\frac{2}{3}AM\left(\text{tính chất đường trung tuyến}\right)\)
\(\Rightarrow GD=\frac{2}{3}AM\) (3)
Từ (1), (2) và (3) suy ra các cạnh của \(\Delta BGD=\frac{2}{3}\) các đường trung tuyến của \(\Delta ABC\)
GM = MD (chứng minh trên)
Nên BM = MD là đường trung tuyến của ∆BGD
\(BM=\frac{1}{2}BC\) (4)
Kẻ đường trung tuyến GE và DF của ∆BGD
\(\Rightarrow FG=\frac{1}{2}BG\)
\(GN=\frac{1}{2}BG\left(\text{tính chất đường trung tuyến}\right)\)
Nên FN = GN
Xét ∆DFG và ∆ANG:
AG = GD (gt)
\(\widehat{DGF}=\widehat{AGN}\left(\text{đối đỉnh}\right)\)
GF = GN (chứng minh trên)
Do đó ∆DFG = ∆ANG (c.g.c)
=> DF = AN
\(AN=\frac{1}{2}AC\left(gt\right)\)
\(\Rightarrow DF=\frac{1}{2}AC\) (5)
BD = CG (chứng minh trên)
\(ED=\frac{1}{2}BD\left(\text{vì E là trung điểm BD}\right)\)
\(GP=\frac{1}{2}CG\left(\text{tính chất đường trung tuyến}\right)\)
=> ED = GP
∆BDM = ∆CGM (chứng minh trên)
\(\Rightarrow\widehat{BDM}=\widehat{CGM}\text{ hay }\widehat{CGM}\)
\(\widehat{CGM}=\widehat{PGA}\left(\text{đối đỉnh}\right)\)
\(\Rightarrow\widehat{EDG}=\widehat{PGA}\)
AG = GD (gt)
=> ∆PGA = ∆EDG (c.g.c)
=> GE = AP
\(\Rightarrow GE=\frac{1}{2}AB\)(6)
Từ (4),(5) và (6) suy ra các đường trung tuyến của ∆BGD bằng một nửa cạnh của ∆ABC.

Tam giác ABC có cạnh huyền PC là 1 cạnh của tam giác PQC
Xét tam giác QMC và tam giác BMN có :
BM=MC
Góc BMN=góc QMC
QM=MN
=>Tam giác BMN=tam giác QMC
=>BN=QC(hai góc tương ứng)
MÌNH CHỈ GIẢI ĐC ĐẾN ĐÂY THÔI

A N C D M E B P G F
a) Gọi AM , BN , CP là các đường trung tuyến của \(\Delta ABC\) . Ta có GD = AG = 2GM và GD = GM + MD nên GM = MD
\(\Delta BMD=\Delta CMG\left(c.g.c\right)\)
\(\Rightarrow BD=CG=\dfrac{2}{3}CP\) (1)
Ta có \(BG=\dfrac{2}{3}BN\) (2)
\(GD=AG=\dfrac{2}{3}AM\) (3)
Từ (1) , (2) , (3) suy ra các cạnh của \(\Delta BGD=\dfrac{2}{3}\) các đường trung truyến của \(\Delta ABC\)
b) Gọi CE , DF là các đường trung tuyến của \(\Delta BGD\) . Từ đây tự chứng minh \(BM=\dfrac{1}{2}BC;GE=\dfrac{1}{2}AB;DF=AN=\dfrac{1}{2}AC\)
Tham khảo: