Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(\begin{array}{l}{\sin ^4}\alpha - {\cos ^4}\alpha = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha - {{\cos }^2}\alpha } \right) = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow {\sin ^2}\alpha - {\cos ^2}\alpha - 1 + 2{\cos ^2}\alpha = 0\\ \Leftrightarrow {\sin ^2}\alpha + {\cos ^2}\alpha - 1 = 0\\ \Leftrightarrow 1 - 1 = 0\\ \Leftrightarrow 0 = 0\end{array}\)
Đẳng thức luôn đúng
b) Ta có:
\(\begin{array}{l}\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{\cos \alpha .\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{1}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\end{array}\)
Đẳng thức luôn đúng

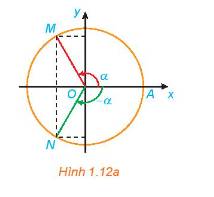
a) Hai điểm M và N đối xứng nhau qua hệ trục Oxy.
Suy ra
\(\cos ( - \alpha )\)=\(\cos \alpha \); \(\sin ( - \alpha )\)= \( - \sin \alpha \)
b) Ta có:
\(\tan ( - \alpha )\) =\( - \tan \alpha \); \(\cot ( - \alpha )\)\( - \cot \alpha \)

a) Ta có: \({\left( {\sin \alpha + \cos \alpha } \right)^2} = {\sin ^2}\alpha + 2\sin \alpha \cos \alpha + {\cos ^2}\alpha = 1 + \sin 2\alpha \;\)
b) \({\cos ^4}\alpha - {\sin ^4}\alpha = \left( {{{\cos }^2}\alpha - {{\sin }^2}\alpha } \right)\left( {{{\cos }^2}\alpha + {{\sin }^2}\alpha } \right) = \cos 2\alpha \;\)

\(P=\frac{sina+cosa}{sina-cosa}=\frac{\frac{sina}{sina}+\frac{cosa}{sina}}{\frac{sina}{sina}-\frac{cosa}{sina}}=\frac{1+cota}{1-cota}=\frac{1+2}{1-2}=-3\)

Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta - \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)

Cách 1:
Ta có: \(tan\alpha=\sqrt{2}\Rightarrow\left\{{}\begin{matrix}\dfrac{sin\alpha}{cos\alpha}=\sqrt{2}\\1+\left(\sqrt{2}\right)^2=\dfrac{1}{cos^2\alpha}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sin\alpha=\sqrt{2}\cdot cos\alpha\\cos^2\alpha=\dfrac{1}{3}\end{matrix}\right.\)
\(P=\dfrac{sin\alpha-cos\alpha}{sin^3\alpha+3cos^3\alpha+2sin\alpha}\)
\(=\dfrac{\sqrt{2}\cdot cos\alpha-cos\alpha}{\left(\sqrt{2}\cdot cos\alpha\right)^3+3cos^3\alpha+2\cdot\sqrt{2}\cdot cos\alpha}\)
\(=\dfrac{cos\alpha\left(\sqrt{2}-1\right)}{2\sqrt{2}\cdot cos^3\alpha+3cos^3\alpha+2\sqrt{2}\cdot cos\alpha}\)
\(=\dfrac{cos\alpha\left(\sqrt{2}-1\right)}{cos\alpha\left(2\sqrt{2}\cdot cos^2\alpha+3cos^2\alpha+2\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{2}-1}{2\sqrt{2}\cdot cos^2\alpha+3cos^2\alpha+2\sqrt{2}}\)
Thay \(cos^2\alpha=\dfrac{1}{3}\) vào \(P\) ta có:
\(P=\dfrac{\sqrt{2}-1}{2\sqrt{2}\cdot\dfrac{1}{3}+3\cdot\dfrac{1}{3}+2\sqrt{2}}=\dfrac{\sqrt{2}-1}{1+\dfrac{8}{3}\sqrt{2}}\)
\(=\dfrac{3\left(\sqrt{2}-1\right)}{3\left(1+\dfrac{8}{3}\sqrt{2}\right)}=\dfrac{3\left(\sqrt{2}-1\right)}{3+8\sqrt{2}}\)
\(=\dfrac{3\left(\sqrt{2}-1\right)}{3+2^3\sqrt{2}}=\dfrac{a\left(\sqrt{b}-1\right)}{a+b^3\sqrt{b}}\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\Rightarrow a+b=5\)
Chọn đáp án A.
Cách 2:
\(P=\dfrac{sin\alpha-cos\alpha}{sin^3\alpha+3cos^3\alpha+2sin\alpha}=\dfrac{\left(sin\alpha-cos\alpha\right)\div cos^3\alpha}{\left(sin^3\alpha+3cos^3\alpha+2sin\alpha\right)\div cos^3\alpha}\)
\(=\dfrac{\dfrac{sin\alpha}{cos^3\alpha}-\dfrac{1}{cos^2\alpha}}{\dfrac{sin^3\alpha}{cos^3\alpha}+3+2\cdot\dfrac{sin\alpha}{cos^3\alpha}}=\dfrac{\dfrac{sin\alpha}{cos\alpha}\cdot\dfrac{1}{cos^2\alpha}-\dfrac{1}{cos^2\alpha}}{tan^3\alpha+3+2\cdot\dfrac{sin\alpha}{cos\alpha}\cdot\dfrac{1}{cos^2\alpha}}\)
\(=\dfrac{tan\alpha\cdot\left(1+tan^2\alpha\right)-\left(1+tan^2\alpha\right)}{tan^3\alpha+3+2tan\alpha\cdot\left(1+tan^2\alpha\right)}\)
Thay \(tan\alpha=\sqrt{2}\) vào ta có:
\(P=\dfrac{\sqrt{2}\cdot\left[1+\left(\sqrt{2}\right)^2\right]-\left[1+\left(\sqrt{2}\right)^2\right]}{\left(\sqrt{2}\right)^3+3+2\sqrt{2}\cdot\left[1+\left(\sqrt{2}\right)^2\right]}=\dfrac{3\sqrt{2}-3}{2\sqrt{2}+3+6\sqrt{2}}\)
\(=\dfrac{3\left(\sqrt{2}-1\right)}{3+8\sqrt{2}}=\dfrac{3\left(\sqrt{2}-1\right)}{3+2^3\sqrt{2}}=\dfrac{a\left(\sqrt{b}-1\right)}{a+b^3\sqrt{b}}\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\Rightarrow a+b=3+2=5\)
Chọn đáp án A

a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\)
c) \(\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\)
d) \(\frac{1}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha \)

Ta có:
a) \(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \sin \alpha \cos \frac{\pi }{6} + \cos \alpha \sin \frac{\pi }{6} = \frac{{\sqrt 6 }}{3}.\frac{{\sqrt 3 }}{2} + \left( { - \frac{1}{{\sqrt 3 }}} \right).\frac{1}{2} = \frac{{ - \sqrt 3 + 3\sqrt 2 }}{6}\)
b) \(\cos \left( {\alpha + \frac{\pi }{6}} \right) = \cos \alpha .\cos \frac{\pi }{6} - \sin \alpha \sin \frac{\pi }{6} = \left( { - \frac{1}{{\sqrt 3 }}} \right).\frac{{\sqrt 3 }}{2} - \frac{{\sqrt 6 }}{3}.\frac{1}{2} = - \frac{{3 + \sqrt 6 }}{6}\)
c) \(\sin \left( {\alpha - \frac{\pi }{3}} \right) = \sin \alpha \cos \frac{\pi }{3} - \cos \alpha \sin \frac{\pi }{3} = \frac{{\sqrt 6 }}{3}.\frac{1}{2} - \left( { - \frac{1}{{\sqrt 3 }}} \right).\frac{{\sqrt 3 }}{2} = \frac{{3 + \sqrt 6 }}{6}\)
d) \(\cos \left( {\alpha - \frac{\pi }{6}} \right) = \cos \alpha \cos \frac{\pi }{6} + \sin \alpha \sin \frac{\pi }{6} = \left( { - \frac{1}{{\sqrt 3 }}} \right).\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 6 }}{3}.\frac{1}{2} = \frac{{ - 3 + \sqrt 6 }}{6}\)
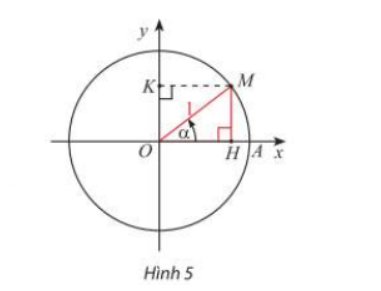
a) Do \(\begin{array}{l}\sin \alpha = MH \Rightarrow {\sin ^2}\alpha = M{H^2}\\\cos \alpha = OH \Rightarrow {\cos ^2}\alpha = O{H^2}\end{array}\)
Áp dụng định lý Py – Ta – Go vào tam giác OMH vuông tại H ta có:
\(\begin{array}{l}M{H^2} + O{H^2} = O{M^2} = 1\\ \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\end{array}\)
b) Chia cả hai vế cho \({\cos ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\end{array}\)
c) Chia cả hai vế cho \({\sin ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow {\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\end{array}\)