Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Gọi phân số cần tìm có dạng là \(\dfrac{a}{12}\)
Theo đề, ta có: \(\dfrac{-2}{3}< \dfrac{a}{12}< \dfrac{-1}{4}\)
\(\Leftrightarrow\dfrac{-8}{12}< \dfrac{a}{12}< \dfrac{-3}{12}\)
\(\Leftrightarrow-8< a< -3\)
\(\Leftrightarrow a\in\left\{-7;-6;-5;-4\right\}\)
Vậy: Các phân số cần tìm là \(\dfrac{-7}{12};\dfrac{-6}{12};\dfrac{-5}{12};\dfrac{-4}{12}\)
b) Gọi phân số cần tìm có dạng là \(\dfrac{15}{a}\left(a\ne0\right)\)
Theo đề, ta có: \(\dfrac{3}{7}< \dfrac{15}{a}< \dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{15}{35}< \dfrac{15}{a}< \dfrac{15}{24}\)
Vậy: Các phân số cần tìm là \(\dfrac{15}{34};\dfrac{15}{33};...;\dfrac{15}{25}\)
a) Gọi tử số của phân số càn tìm là x
Theo đề bài ta có:
\(\dfrac{-2}{5}< \dfrac{x}{30}< \dfrac{-1}{6}\)
\(\Rightarrow\dfrac{-12}{30}< \dfrac{x}{30}< \dfrac{-5}{30}\)
\(\Rightarrow x=\left\{-11;-10;-9;-8;-7;-6\right\}\)
Gọi tập hợp các tử số của số hữu tỉ đó là x
\(\Rightarrow\dfrac{-7}{10}< \dfrac{x}{15}< \dfrac{-9}{20}\Leftrightarrow\dfrac{-42}{60}< \dfrac{4x}{60}< \dfrac{-27}{60}\Leftrightarrow-42< 4x< -27\)
\(\Leftrightarrow x\in\left\{-10;-9;-8;-7;-6\right\}\)
Vậy các số hữu tỉ cần tìm là: \(S=\left\{-\dfrac{10}{15};-\dfrac{9}{15};-\dfrac{8}{15};-\dfrac{7}{15};-\dfrac{6}{15}\right\}\)
Gọi các số hữu tỉ cần tìm có dạng là: \(\dfrac{x}{15}\)
Theo đề, ta có: \(\dfrac{-7}{10}< \dfrac{x}{15}< -\dfrac{9}{20}\)
\(\Leftrightarrow\dfrac{-42}{60}< \dfrac{4x}{60}< \dfrac{-27}{60}\)
\(\Leftrightarrow4x\in\left\{-40;-36;-32;-28\right\}\)
hay \(x\in\left\{-10;-9;-8;-7\right\}\)
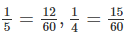
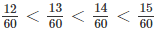
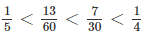
a: Gọi tử là x
Theo đề, ta có: \(\dfrac{4}{13}< \dfrac{x}{20}< \dfrac{5}{13}\)
=>80<13x<100
=>x=5
b: Vì 5/7<5/6 nên không có phân số nào lớn hơn 5/7 và nhỏ hơn 5/6