Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì 18/91 < 18/90 =1/5
23/114>23115=1/5
vậy 18/91<1/5<23/114
suy ra 18/91<23/114
vì 21/52=210/520
Mà 210/520=1-310/520
213/523=1-310/523
310/520>310/523
vậy 210/520<213/523
suy ra 21/52<213/523

d, Vì B=10^1993+1/10^1992+1 > 1 =>10^1993+1/10^1992+1>10^1993+1+9/10^1992+1+9 = 10^1993+10/10^1992+10= 10. (10^1992+1)/10. (10^1991+1) = 10^1992+1/10^1991+1=A Vậy A=B
cau d B>1 ta co tinh chat (\(\dfrac{a}{b}>\dfrac{a+m}{b+m}\) ) B> \(\dfrac{10^{1993}+1+9}{10^{1992}+1+9}\)\(=\dfrac{10^{1993}+10}{10^{1992}+10}\)=\(\dfrac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}\)=\(\dfrac{10^{1992}+1}{10^{1991}+1}\)=A
Suy ra B>A(chuc ban hoc goi nhe)

a, \(A-B=\frac{3}{8^3}+\frac{7}{8^4}-\frac{7}{8^3}-\frac{3}{8^4}==\left(\frac{7}{8^4}-\frac{3}{8^4}\right)-\left(\frac{7}{8^3}-\frac{3}{8^3}\right)=\frac{4}{8^4}-\frac{4}{8^3}< 0\)
Vậy A < B
b, \(A=\frac{10^7+5}{10^7-8}=\frac{10^7-8+13}{10^7-8}=1+\frac{13}{10^7-8}\)
\(B=\frac{10^8+6}{10^8-7}=\frac{10^8-7+13}{10^8-7}=1+\frac{13}{10^8-7}\)
Vì \(10^7-8< 10^8-7\Rightarrow\frac{1}{10^7-8}>\frac{1}{10^8-7}\Rightarrow\frac{13}{10^7-8}>\frac{13}{10^8-7}\Rightarrow A>B\)
c,Áp dụng nếu \(\frac{a}{b}>1\Rightarrow\frac{a}{b}>\frac{a+n}{a+n}\) có:
\(B=\frac{10^{1993}+1}{10^{1992}+1}>\frac{10^{1993}+1+9}{10^{1992}+1+9}=\frac{10^{1993}+10}{10^{1992}+10}=\frac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}=\frac{10^{1992}+1}{10^{1991}+1}=A\)
Vậy A < B

\(a.\dfrac{3}{5}-\dfrac{-7}{10}-\dfrac{13}{-20}=\dfrac{12}{20}-\dfrac{-14}{20}-\dfrac{-13}{20}=\dfrac{12-\left(-14\right)-\left(-13\right)}{20}=\dfrac{39}{20}\)
\(b.\dfrac{3}{4}+\dfrac{-1}{3}-\dfrac{5}{18}=\dfrac{3}{4}+\left(\dfrac{-6}{18}-\dfrac{5}{18}\right)=\dfrac{3}{4}+\dfrac{-11}{18}=\dfrac{27}{36}-\dfrac{-22}{36}=\dfrac{49}{36}\)
\(c.\dfrac{3}{13}-\dfrac{5}{-8}+\dfrac{-1}{2}=\dfrac{3}{13}-\left(\dfrac{5}{-8}+\dfrac{-4}{8}\right)=\dfrac{3}{13}-\dfrac{1}{8}=\dfrac{24}{104}-\dfrac{13}{104}=\dfrac{11}{104}\)
\(d.\dfrac{1}{2}+\dfrac{1}{-3}=\dfrac{3}{6}+\dfrac{-2}{6}=\dfrac{1}{6}\)
\(a,\dfrac{3}{5}-\dfrac{-7}{10}-\dfrac{13}{-20}\)
\(=\dfrac{12}{20}+\dfrac{14}{20}+\dfrac{13}{20}\)
\(=\dfrac{12+14+13}{20}\)
\(=\dfrac{39}{20}\)
\(b,\dfrac{3}{4}+\dfrac{-1}{3}-\dfrac{5}{18}\)
\(=\dfrac{27}{36}+\dfrac{-12}{36}-\dfrac{10}{36}\)
\(=\dfrac{27+\left(-12\right)-10}{36}\)
\(=\dfrac{5}{36}\)
\(c,\dfrac{3}{13}-\dfrac{5}{-8}+\dfrac{-1}{2}\)
\(=\dfrac{24}{104}-\dfrac{-65}{104}+\dfrac{-52}{104}\)
\(=\dfrac{24-\left(-65\right)+\left(-52\right)}{104}\)
\(=\dfrac{37}{104}\)
\(d,\dfrac{1}{2}+\dfrac{1}{-3}\)
\(=\dfrac{3}{6}+\dfrac{-2}{6}\)
\(=\dfrac{3+\left(-2\right)}{6}\)
\(=\dfrac{1}{6}\)

a) \(\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}.....\dfrac{779}{780}\)\(=\)

a: \(\Leftrightarrow70+18< x< 120+126+70\)
=>88<x<316
hay \(x\in\left\{89;90;...;315\right\}\)
b: \(\Leftrightarrow-\dfrac{9}{3}< x< \dfrac{8}{5}+\dfrac{9}{5}=\dfrac{17}{5}\)
=>-3<x<3,4
hay \(x\in\left\{-2;-1;0;1;2;3\right\}\)

1)
a)
\(\dfrac{-21}{28}=\dfrac{\left(-21\right):7}{28:7}=\dfrac{-3}{4}\\ \dfrac{-39}{52}=\dfrac{\left(-39\right):13}{52:13}=\dfrac{-3}{4}\)
Vì \(\dfrac{-3}{4}=\dfrac{-3}{4}\) nên \(\dfrac{-21}{28}=\dfrac{-39}{52}\)
b)
\(\dfrac{-1717}{2323}=\dfrac{\left(-17\right)\cdot101}{23\cdot101}=\dfrac{-17}{23}\\ \dfrac{-171717}{232323}=\dfrac{\left(-17\right)\cdot10101}{23\cdot10101}=\dfrac{-17}{23}\)
Vì \(\dfrac{-17}{23}=\dfrac{-17}{23}\) nên \(\dfrac{-1717}{2323}=\dfrac{-171717}{232323}\)
2)
Theo tính chất cơ bản của phân số ta có: \(\dfrac{a}{b}=\dfrac{a\cdot m}{b\cdot m}\) mà \(m\ne n\)
nên không thể.
Trường hợp duy nhất là khi \(a=0\)
Khi đó: \(\dfrac{a}{b}=\dfrac{0}{b}=\dfrac{0\cdot m}{b\cdot n}=\dfrac{0}{b\cdot n}=0\)
3)
Gọi ƯCLN\(\left(12n+1,30n+2\right)\) là \(d\)
Ta có:
\(12n+1⋮d\\ \Rightarrow5\cdot\left(12n+1\right)⋮d\left(1\right)\\ \Leftrightarrow60n+5⋮d\\ 30n+2⋮d\\ \Rightarrow2\cdot\left(30n+2\right)⋮d\\ \Leftrightarrow60n+4⋮d\left(2\right)\)
Từ (1) và (2) ta có:
\(\left(60n+5\right)-\left(60n+4\right)⋮d\\ \Leftrightarrow1⋮d\\ \Rightarrow d=1\)
Vậy ƯCLN\(\left(12n+1,30n+2\right)=1\)
Mà hai số có ƯCLN = 1 thì hai số đó nguyên tố cùng nhau và không có ước chung nào khác
\(\Rightarrow\dfrac{12n+1}{30n+2}\)tối giản



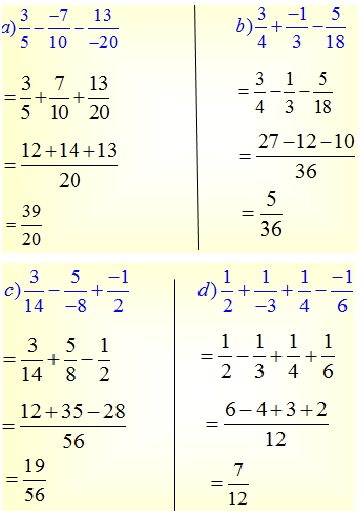
a.
$10A=\frac{10^{2021}+10}{10^{2021}+1}=1+\frac{9}{10^{2021}+1}<1+\frac{9}{10^{2020}+1}=\frac{10+10^{2020}}{10^{2020}+1}=10B$
$\Rightarrow A< B$
b.
\(C=2(\frac{2}{3.5}+\frac{2}{5.7}+....+\frac{2}{97.99})=2(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+....+\frac{1}{97}-\frac{1}{99})\)
\(=2(\frac{1}{3}-\frac{1}{99})=\frac{64}{99}\)
\(D=6(\frac{3}{2.5}+\frac{3}{5.8}+....+\frac{3}{203.206})=6(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+...+\frac{1}{203}-\frac{1}{206})\)
$=6(\frac{1}{2}-\frac{1}{206})=\frac{306}{103}$
$C:D=\frac{64}{99}: \frac{306}{103}=\frac{3296}{15147}$
c.
\(A=\frac{12n}{3n+3}=\frac{12n}{3(n+1)}=\frac{4n}{n+1}=\frac{4(n+1)-4}{n+1}=4-\frac{4}{n+1}\)
Để $A$ nguyên thì $\frac{4}{n+1}$ nguyên
$\Rightarrow n+1$ là ước của $4$
$\Rightarrow n+1\in\left\{\pm 1; \pm 4\right\}$
$\Rightarrow n\in\left\{0; -2; 3; -5\right\}$