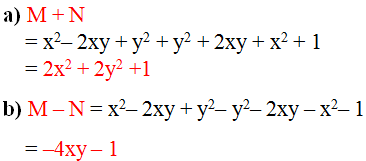K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LQ
26 tháng 4 2017
\(a;M\left(x\right)+N\left(x\right)=\left(2x^3-5x^2+x-2\right)+\left(-3x^3+5x^2-x+1\right)\)
\(=2x^3-5x^2+x-2-3x^3+5x^2-x+1\)
\(=-x^3-1\)
\(b;M\left(x\right)-N\left(x\right)=\left(2x^3-5x^2+x^2-2\right)-\left(-3x^3+5x^2-x+1\right)\)
\(=2x^3-5x^2+x-2+3x^3-5x^2+x-1\)
\(=5x^3-10x^2+2x-3\)
\(c;3N\left(x\right)-2M\left(x\right)=3\left(2x^3-5x^2+x-2\right)-2\left(-3x^3+5x^2-x+1\right)\)
\(=6x^3-15x^2+3x-6+6x^3-10x^2+2x-2\)
\(=12x^3-25x^2+5x-8\)
8 tháng 10 2017
Do theo đề bài: \(\frac{a}{m}=\frac{b}{n}=\frac{c}{p}=-4\)
\(\Rightarrow\left(\frac{a}{m}\right)^3=\left(\frac{b}{n}\right)^3=\left(\frac{c}{p}\right)^3=\left(-4\right)^3\)
\(\Rightarrow\frac{a^3}{m^3}=\frac{b^3}{n^3}=\frac{c^3}{p^3}=-64\)
\(\Rightarrow\frac{-a^3}{m^3}=\frac{3\cdot b^3}{\left(-3\right)\cdot n^3}=\frac{\left(-2\right)\cdot c^3}{2\cdot p^3}=64\) ( 1 )
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{-a^3}{m^3}=\frac{3\cdot b^3}{\left(-3\right)\cdot n^3}=\frac{\left(-2\right)\cdot c^3}{2\cdot p^3}=\frac{\left(-a^3\right)+3\cdot b^3+\left(-2\right)\cdot c^3}{m^3+\left(-3\right)\cdot n^3+2\cdot p^3}=\frac{-a^3+3\cdot b^3-2\cdot c^3}{m^3-3.n^3+2\cdot p^3}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra: \(\frac{-a^3+3\cdot b^3-2\cdot c^3}{m^3-3.n^3+2\cdot p^3}=64\)
19 tháng 9 2018
M + N = \(x^2-2xy+y^2\)+\(y^2+2xy+x^2+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2+y^2\right)+1\)
= \(2x^2+2y^2+1\)
M - N = \(x^2-2xy+y^2-y^2+2xy+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2-y^2\right)+1\)
= \(2x^2+1\)
13 tháng 6 2016
a) vì a<b => 2a<a + b ; c < d => 2c < c + d ; m<n => 2m< m + n
=> 2a + 2c + 2m = 2 (a + c + m) < ( a + b + c + m + n)
=> \(\frac{a+c+m}{a+b+c+m+n}< \frac{1}{2}\left(đccm\right)\)
t i c k nha!! 4545654756678769780
13 tháng 6 2016
Ta có:\(1\le a;2\le b;3\le c;4\le d;5\le m;6\le n\)
\(\Rightarrow\hept{\begin{cases}a+c+m\ge1+3+5=9\\a+b+c+m+n=1+2+3+5+6=17\end{cases}}\)
\(\Rightarrow\frac{a+c+m}{a+b+c+m+n}\ge\frac{9}{17}>\frac{9}{18}=\frac{1}{2}\)
b,Tương tự
DD
18 tháng 5 2017
\(M\left(x\right)+N\left(x\right)\)
\(=5x^3-x^2-4+2x^4-2x^2+2x+1\)
\(=2x^4+5x^3-3x^2+2x-3\)
\(M\left(x\right)-N\left(x\right)\)
\(=5x^3-x^2-4-\left(2x^4-2x^2+2x+1\right)\)
\(=5x^3-x^2-4-2x^4+2x^2-2x-1\)
\(=-2x^4+5x^3+x^2-2x-5\)
\(M\left(x\right)+P\left(x\right)=N\left(x\right)\)
\(\Rightarrow P\left(x\right)=N\left(x\right)-M\left(x\right)\)
\(\Rightarrow P\left(x\right)=2x^4-2x^2+2x+1-\left(5x^3-x^2-4\right)\)
\(\Rightarrow P\left(x\right)=2x^4-2x^2+2x+1-5x^3+x^2+4\)
\(\Rightarrow P\left(x\right)=2x^4-5x^3-x^2+2x+5\)
TT
1
15 tháng 1 2017
Ta có :
\(a< b\Rightarrow2a< a+b\) \(\left(1\right)\)
\(c< d\Rightarrow2c< c+d\) \(\left(2\right)\)
\(m< n\Rightarrow2m< m+n\) \(\left(3\right)\)
Cộng ba bất đẳng thức cùng chiều \(\left(1\right),\left(2\right),\left(3\right)\) , ta được :
\(2a+2c+2m< a+b+c+d+m+n\)
\(\Rightarrow\frac{a+c+m}{a+b+c+d+m+n}< \frac{1}{2}\)
Vậy : \(\frac{a+c+m}{a+b+c+d+m+n}< \frac{1}{2}\)