K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
19 tháng 12 2017
Lời giải:
\(a+b=3\Rightarrow a+(b-2)=1\Rightarrow b-2=1-a\)
Ta có:
\(f(x)=\frac{9^x}{9^x+3}\Rightarrow f(a)=\frac{9^a}{9^a+3}\) (1)
\(f(b-2)=f(1-a)=\frac{9^{1-a}}{9^{1-a}+3}=\frac{9}{9^a\left(\frac{9}{9^a}+3\right)}\)
\(=\frac{9}{9+3.9^a}=\frac{3}{3+9^a}\) (2)
Từ (1),(2) suy ra \(f(a)+f(b-2)=\frac{9^a}{9^a+3}+\frac{3}{3+9^a}=\frac{9^a+3}{9^a+3}=1\)
Đáp án A
AH
Akai Haruma
Giáo viên
20 tháng 3 2017
Lời giải:
Gọi \(D=(a,b,c)\). Tính toán: \(\left\{\begin{matrix} \overrightarrow{AB}=(2,2,1)\\ \overrightarrow{BC}=(2,-7,1)\\ \overrightarrow{AC}=(4,-5,2)\end{matrix}\right.\)
Thấy \(\overrightarrow{AB}.\overrightarrow{AC}=0\Rightarrow\overrightarrow{AB}\perp \overrightarrow{AC}\) nên \(A,B,C,D\) là bốn đỉnh của hình chữ nhật $ABDC$
Ta có \(\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{AD}\Leftrightarrow (4,-5,2)+(2,2,1)=(a-2,b-1,c+3)\)
\(\Leftrightarrow \left\{\begin{matrix} a-2=6\\ b-1=-3\\ c+3=3\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=8\\ b=-2\\ c=0\end{matrix}\right.\)
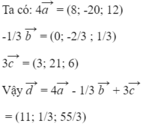
Chọn B