K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CT
0
KT
2
2 tháng 4 2015
A=\(\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right)...\left(1-\frac{2010}{2010}\right)\left(1-\frac{2011}{2010}\right)\)
A=\(\frac{2009}{2010}.\frac{2008}{2010}...0.\frac{-1}{2010}\)
A=0
M
2
D
15 tháng 4 2017
Ta có:\(1-\frac{2010}{2010}=1-1=0\)
Tích A= (1-1/2010).(1-2/2010).(1-3/2010)....(1-2011/2010) chứa thừa số \(1-\frac{2010}{2010}=0\)
Vậy tích A=(1-1/2010).(1-2/2010).(1-3/2010)....(1-2011/2010)=0(Vì có chứa thừa số 0)
LT
1
LT
1
26 tháng 6 2022
\(A=\dfrac{2009}{2010}\cdot\dfrac{2008}{2010}\cdot...\cdot\dfrac{2}{2010}\cdot\dfrac{1}{2010}\cdot\dfrac{0}{2010}\cdot\dfrac{-1}{2010}\)
=0
5 tháng 12 2022
Bài 2:
1: \(2A=2+2^2+...+2^{2011}\)
=>\(A=2^{2011}-1>B\)
2: \(A=\left(2010-1\right)\left(2010+1\right)=2010^2-1< B\)
3: \(A=1000^{10}\)
\(B=2^{100}=1024^{10}\)
mà 1000<1024
nên A<B
5: \(A=3^{450}=27^{150}\)
\(B=5^{300}=25^{150}\)
mà 27>25
nên A>B
30 tháng 12 2016
1)
a) A = 21 + 22 + … + 22010
= (21 + 22) + (23 + 24) + … + (22009 + 22010)
= 2(1 + 2) + 23(1 + 2) + … + 22009(1 + 2)
= 2.3 + 23.3 + … + 22009.3
Vì 3 chia hết cho 3 nên A chia hết cho 3.
A = 21 + 22 + … + 22010
= (21 + 22 + 23) + (24 + 25 + 26) + … + (22008 + 22009 + 22010)
= 2(1 + 2 + 22) + 24(1 + 2 + 22) + … + 22008(1 + 2 + 22)
= 2.7 + 24.7 + … + 22008.7
Vì 7 chia hết cho 7 nên A chia hết cho 7.
b) B = 31 + 32 + … + 32010
= (31 + 32 )+ (33 + 34) + (35 + 36) + … + (32009 + 32010)
= 3(1 + 3) + 33(1 + 3) + … + 32009(1 + 3)
= 3.4+ 33.4 + … + 32009.4
Vì 4 chia hết cho 4 nên B chia hết cho 4.
B = 31 + 32 + … + 32010
= (31 + 32 + 33) + (34 + 35 + 36) + … + (32008 + 32009 + 32010)
= 3(1 + 3 + 32) + 34(1 + 3 + 32) + … + 32008(1 + 3 + 32)
= 3.13 + 34.13 + … + 32008.13
Vì 13 chia hết cho 13 nên B chia hết cho 13.
c) C = 51 + 52 + … + 52010
= (51 + 52 +53 + 54) + … + (52007 + 52008 + 52009 + 52010)
= 5(1 + 5 + 52 + 53) + … + 52007(1 + 5 + 52 + 53)
= 5.156 + … + 52007.156
Vì 156 chia hết cho 6, 12 nên C chia hết cho 6 và 12.
2)
a) Ta có: A = 20 + 21 + 22 + … + 22010 = 22011 – 1
Vậy A = B ( vì đều bằng 22011 – 1 )
b) Ta có: A = 2009.2011 = 2009.(2010 + 1) = 2009.2010 + 2009
B = 20102 = 2010.2010 = (2009 + 1).2010 = 2009.2010 + 2010
Vì ở A và B đều có 2009.2010 mà 2009 < 2010 nên A < B.
c) Ta có: A = 1030 = 103.10 = (103)10 = 10010
B = 2100 = 210.10 = (210)10 = 102410
Vì 10010 < 102410 nên A < B.
d) Ta có: A = 333444 = 3334.111 = (3334)111
B = 444333 = 4443.111 = (4443)111
Ta so sánh 3334 và 4443
3334 = (3.111)4 = 34.1114 = 81.111.1113
4443 = (4.111)3 = 43.1113 = 64.1113
Vì 81.111 > 64 => 3334 > 4443 => (3334)111 > (4443)111 => A > B.
30 tháng 12 2016
2)a) Ta có: A = 20 + 21 + 22 + … + 22010 = 22011 – 1
Vậy A = B ( vì đều bằng 22011 – 1 )
b) Ta có: A = 2009.2011 = 2009.(2010 + 1) = 2009.2010 + 2009
B = 20102 = 2010.2010 = (2009 + 1).2010 = 2009.2010 + 2010
Vì ở A và B đều có 2009.2010 mà 2009 < 2010 nên A < B.
c) Ta có: A = 1030 = 103.10 = (103)10 = 10010
B = 2100 = 210.10 = (210)10 = 102410
Vì 10010 < 102410 nên A < B.
d) Ta có: A = 333444 = 3334.111 = (3334)111
B = 444333 = 4443.111 = (4443)111
Ta so sánh 3334 và 4443
3334 = (3.111)4 = 34.1114 = 81.111.1113
4443 = (4.111)3 = 43.1113 = 64.1113
Vì 81.111 > 64 => 3334 > 4443 => (3334)111 > (4443)111 => A > B.
2 tháng 5 2017
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right).....\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right).....\left(1-\frac{2010}{2010}\right).\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right).....\left(1-1\right).\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right)\left(1-\frac{2}{2010}\right)\left(1-\frac{3}{2010}\right)....0.\left(1-\frac{2011}{2010}\right)\)
\(A=0\)
2 tháng 5 2017
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right)...\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right)...\left(1-\frac{2010}{2010}\right).\left(1-\frac{2011}{2010}\right)\)
\(A=\left(1-\frac{1}{2010}\right).\left(1-\frac{2}{2010}\right).\left(1-\frac{3}{2010}\right)...0.\left(1-\frac{2011}{2010}\right)\)
\(\Rightarrow A=0\)
( Vì 0 nhân với số nào cũng bằng 0 )
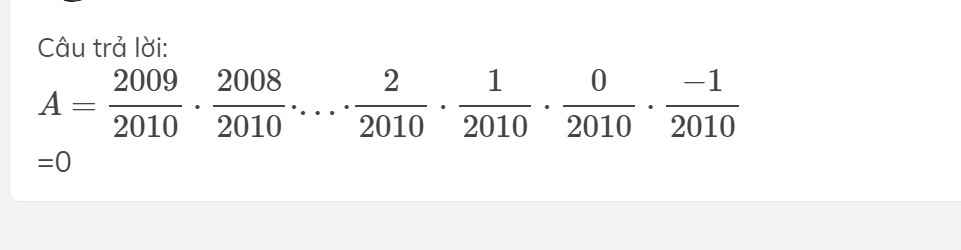
trong vòng 30 giây nhá