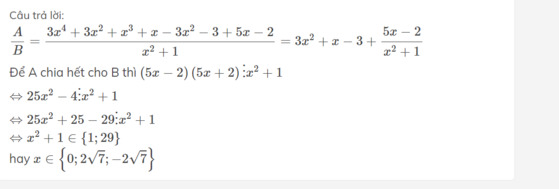Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

â. (A+B)2 = A2+2AB+B2
b. A2 – B2= (A-B)(A+B)
c. (A – B)2= A2 – 2AB+ B2
d. A3 + B3= (A+B)(A2- AB +B2)
e. cái này bạn phải chú ý cách sắp xếp mà sx nó lại \(x^6-2x^3y+y^2\) (A – B)2= A2 – 2AB+ B2
f. (A+B)3= A3+3A2B +3AB2+B3
a) x2+6xy+9y2 = x2+2.x.3y+(3y)2 = (x+3y)2
b) x2-\(\dfrac{1}{4}\)= x2- (\(\dfrac{1}{2}\))2 = (x-\(\dfrac{1}{2}\))(x+\(\dfrac{1}{2}\))
c) x2 -10x+25 = x2 -2.x.5+52 = (x-5)2
d) 8x3+27y3 = (2x)3+(3y)3 = (2x+3y)[(2x)2 -2x.3y+(3y)2]
e) x6 +y2 -2x3y = x6-2x3y +y2 = (x3)2 -2x3y +y2 = (x3 -y)2
f) x3 +9x2y +27xy2 +27y3 = x3 +3.x2.3y +3.x.(3y)2 +(3y)3 = (x+3y)3

Bài 3:
a) ta có: \(A=x^2+4x+9\)
\(=x^2+4x+4+5=\left(x+2\right)^2+5\)
Ta có: \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi
\(\left(x+2\right)^2=0\Leftrightarrow x+2=0\Leftrightarrow x=-2\)
Vậy: GTNN của đa thức \(A=x^2+4x+9\) là 5 khi x=-2
b) Ta có: \(B=2x^2-20x+53\)
\(=2\left(x^2-10x+\frac{53}{2}\right)\)
\(=2\left(x^2-10x+25+\frac{3}{2}\right)\)
\(=2\left[\left(x-5\right)^2+\frac{3}{2}\right]\)
\(=2\left(x-5\right)^2+2\cdot\frac{3}{2}\)
\(=2\left(x-5\right)^2+3\)
Ta có: \(\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-5\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi
\(2\left(x-5\right)^2=0\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x-5=0\Leftrightarrow x=5\)
Vậy: GTNN của đa thức \(B=2x^2-20x+53\) là 3 khi x=5
c) Ta có : \(M=1+6x-x^2\)
\(=-x^2+6x+1\)
\(=-\left(x^2-6x-1\right)\)
\(=-\left(x^2-6x+9-10\right)\)
\(=-\left[\left(x-3\right)^2-10\right]\)
\(=-\left(x-3\right)^2+10\)
Ta có: \(\left(x-3\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-3\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-3\right)^2+10\le10\forall x\)
Dấu '=' xảy ra khi
\(-\left(x-3\right)^2=0\Leftrightarrow\left(x-3\right)^2=0\Leftrightarrow x-3=0\Leftrightarrow x=3\)
Vậy: GTLN của đa thức \(M=1+6x-x^2\) là 10 khi x=3
Bài 2:
a) \(\left(x+y\right)^2+\left(x^2-y^2\right)\)
\(=\left(x+y\right)^2+\left(x-y\right).\left(x+y\right)\)
\(=\left(x+y\right).\left(x+y+x-y\right)\)
\(=\left(x+y\right).2x\)
c) \(x^2-2xy+y^2-z^2+2zt-t^2\)
\(=\left(x^2-2xy+y^2\right)-\left(z^2-2zt+t^2\right)\)
\(=\left(x-y\right)^2-\left(z-t\right)^2\)
\(=\left[x-y-\left(z-t\right)\right].\left(x-y+z-t\right)\)
\(=\left(x-y-z+t\right).\left(x-y+z-t\right)\)
Chúc bạn học tốt!

https://olm.vn/hoi-dap/question/125053.html
BN THAM KHỎA LINK NÀY NHÉ BÀI NÀY TƯƠNG TỰ NAK

\(a,\\ T=\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{4}\right)+\left(1-\dfrac{1}{8}\right)+...+\left(1-\dfrac{1}{4096}\right)\\ T=\left(1+1+1+...+1\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{4096}\right)\)
Gọi \(D=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{4096}\)
\(2D=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2048}\\ 2D-D=\left(1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2048}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{4096}\right)\\ D=1-\dfrac{1}{4096}\)
(mk nhớ có cách khác rất hay nhưng quên mất rồi)
Thay \(D\) vào ta được
\(T=\left(1+1+1+...+1\right)-\left(1-\dfrac{1}{4096}\right)\\ T=12-\left(1-\dfrac{1}{4096}\right)\\ T=12-1+\dfrac{1}{4096}\\ T=11\dfrac{1}{4096}\)

a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-1=4-3x\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)