K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DG
2
TN
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 12 2022
a, 3x ( y+1) + y + 1 = 7
(y+1)(3x +1) =7
th1 : \(\left\{{}\begin{matrix}y+1=1\\3x+1=7\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=0\\x=2\end{matrix}\right.\)
th2: \(\left\{{}\begin{matrix}y+1=-1\\3x+1=-7\end{matrix}\right.\)=> x = -8/3 (loại)
th3: \(\left\{{}\begin{matrix}y+1=7\\3x+1=1\end{matrix}\right.\)=> \(\left\{{}\begin{matrix}y=6\\x=0\end{matrix}\right.\)
th 4 : \(\left\{{}\begin{matrix}y+1=-7\\3x+1=-1\end{matrix}\right.\)=> x=-2/3 (loại)
Vậy (x,y)= (2 ;0); (0; 6)
b, xy - x + 3y - 3 = 5
(x( y-1) + 3( y-1) = 5
(y-1)(x+3) = 5
th1: \(\left\{{}\begin{matrix}y-1=1\\x+3=5\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=2\\x=8\end{matrix}\right.\)
th2: \(\left\{{}\begin{matrix}y-1=-1\\x+3=-5\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=0\\x=-8\end{matrix}\right.\)
th3: \(\left\{{}\begin{matrix}y-1=5\\x+3=1\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=6\\x=-2\end{matrix}\right.\)
th4: \(\left\{{}\begin{matrix}y-1=-5\\x+3=-1\end{matrix}\right.\) => \(\left\{{}\begin{matrix}y=-4\\x=-4\end{matrix}\right.\)
vậy (x, y) = ( 8; 2); ( -8; 0); (-2; 6); (-4; -4)
c, 2xy + x + y = 7 => y = \(\dfrac{7-x}{2x+1}\) ; y ϵ Z ⇔ 7-x ⋮ 2x+1
⇔ 14 - 2x ⋮ 2x + 1 ⇔ 15 - 2x - 1 ⋮ 2x + 1
th1 : 2x + 1 = -1=> x = -1; y = \(\dfrac{7-(-1)}{-1.2+1}\) = -8
th2: 2x+ 1 = 1=> x =0; y = 7
th3: 2x+1 = -3 => x = x=-2 => y = \(\dfrac{7-(-2)}{-2.2+1}\) = -3
th4: 2x+ 1 = 3 => x = 1 => y = \(\dfrac{7+1}{2.1+1}\) = 2
th5: 2x + 1 = -5 => x = -3=> y = \(\dfrac{7-(-3)}{-3.2+1}\) = -2
th6: 2x + 1 = 5 => x = 2; ; y = \(\dfrac{7-2}{2.2+1}\) =1
th7 : 2x + 1 = -15 => x = -8; y = \(\dfrac{7-(-8)}{-8.2+1}\) = -1
th8 : 2x+1 = 15 => x = 7; y = \(\dfrac{7-7}{2.7+1}\) = 0
kết luận
(x,y) = (-1; -8); (0 ;7); ( -2; -3) ; ( 1; 2); ( -3; -2); (2;1); (-8;-1);(7;0)
26 tháng 12 2022
3xy−2x+5y=293xy−2x+5y=29
9xy−6x+15y=879xy−6x+15y=87
(9xy−6x)+(15y−10)=77(9xy−6x)+(15y−10)=77
3x(3y−2)+5(3y−2)=773x(3y−2)+5(3y−2)=77
(3y−2)(3x+5)=77(3y−2)(3x+5)=77
⇒(3y−2)⇒(3y−2) và (3x+5)(3x+5) là Ư(77)=±1,±7,±11,±77Ư(77)=±1,±7,±11,±77
Ta có bảng giá trị sau:
Do x,y∈Zx,y∈Z nên (x,y)∈{(−4;−3),(−2;−25),(2;3),(24;1)}
TC
1
AH
Akai Haruma
Giáo viên
24 tháng 9 2023
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: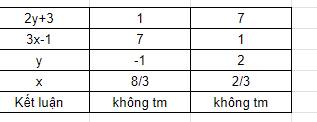
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
QA
0
TH
5
15 tháng 1 2017
Ta có :
2(x - xy + y) = 2.3
<=> 2x - 2xy + 2y = 6
<=> 2x - (2xy - 2y ) = 6
<=> 2x - 2y(2x - 1) = 6
<=> (2x - 1) - 2y(2x - 1) = 6 - 1
<=> (2x - 1)(1 - 2y) = 5
=> 2x - 1 và 1 - 2y là ước của 5
Ư(5) = { - 5 ; - 1 ; 1 ; 5 }
Nếu 2x - 1 = - 5 thì 1 - 2y = - 1 => x = - 2 thì y = 1
Nếu 2x - 1 = - 1 thì 1 - 2y = - 5 => x = 0 thì y = 3
Nếu 2x - 1 = 1 thì 1 - 2y = 5 => x = 1 thì y = - 2 ( loại vì ko TM )
Nếu 2x - 1 = 5 thì 1 - 2y = 1 => x = 3 thì y = 0
Vậy ( x;y ) = { (-2;1);(0;3);(3;0)}
Câu b đợi tôi nghĩ đã :))
15 tháng 1 2017
b )
x2 - 3xy + x - 3y = 7
<=> x(x - 3y) + (x - 3y) = 7
<=> (x + 1)(x - 3y) = 7
=> x + 1 và x - 3y là ước của 7
=> Ư(7) = { - 7; - 1; 1; 7 }
Nếu x + 1 = - 7 thì x - 3y = - 1 => x = - 8 thì y = -7/3 ( loại vì y là số nguyên )
Nếu x - 1 = - 1 thì x - 3y = - 7 => x = 0 thì y = 7/3 ( loại )
Nếu x - 1 = 1 thì x - 3y = 7 => x = 2 thì y = 5/3 ( loại )
Nếu x - 1 = 7 thì x - 3y = 1 => x = 8 thì y = 7/3 ( loại )
Vậy ko có cặp ( x;y ) nào thỏa mãn phương trình trên
Mình ko chắc về lời giải này lắm :))
MT
1
TH
30 tháng 11 2016
ta có: 3xy-x+3y-1=15<=>(3xy+3y)-(x+1)=15<=>3y(x+1)-(x+1)=15<=>(x+1)(3y-1)=15=>x+1 và 3y-1 thuộc Ư(15)
từ đó tính tiếp