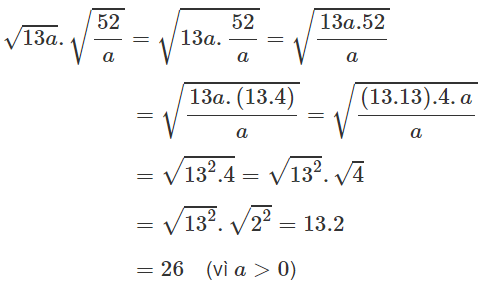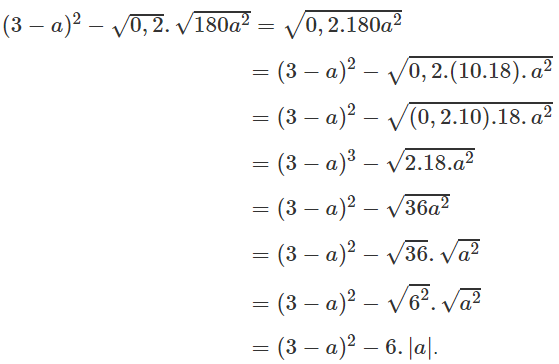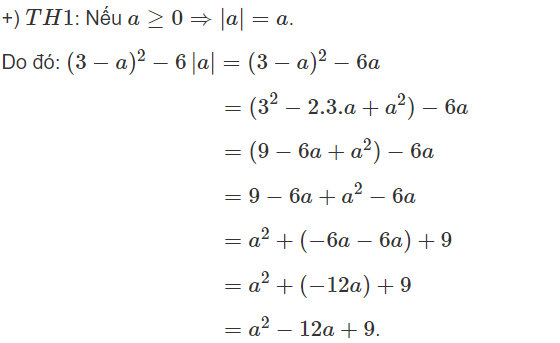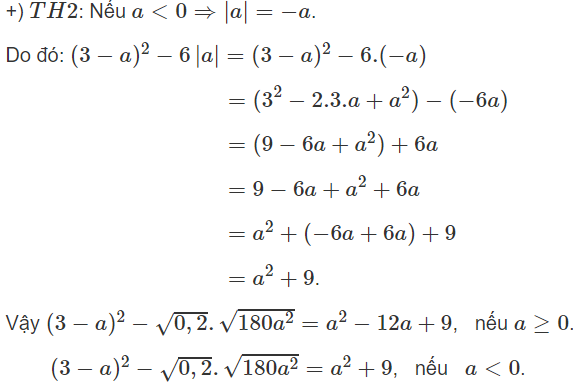K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 4 2021
a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)
25 tháng 6 2019
1) \(\sqrt{\frac{24}{3}}\cdot\sqrt{\frac{3a}{8}}=\sqrt{\frac{72a}{24}}=\sqrt{3a}\)
2) \(\sqrt{13a}\cdot\sqrt{\frac{52}{a}}=\sqrt{\frac{13a\cdot52}{a}}=\sqrt{676}=26\)
3) \(\sqrt{5a}\cdot\sqrt{45a}-3a=\sqrt{225a^2}-3a=15a-3a=12a\)
4) \(\left(3-a\right)^2-\sqrt{0,2}\cdot\sqrt{180a^2}=a^2-6a+9-\sqrt{36a^2}=a^2-6a+9-6a=a^2-12a+9\)
CM
2 tháng 11 2017
a) Ta có:
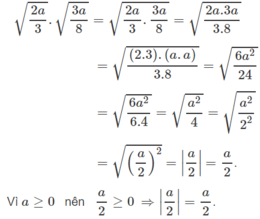
b) Ta có:
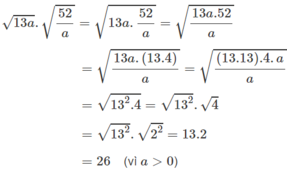
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:
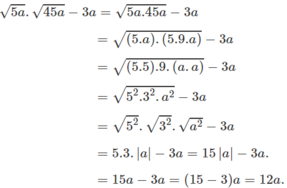
(Vì a ≥ 0 nên |a| = a)
d) Ta có:
A
9 tháng 6 2019
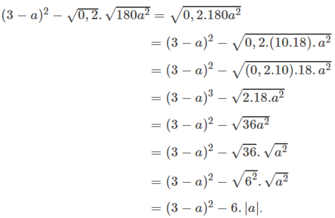
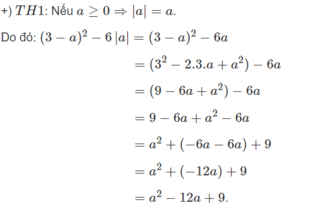
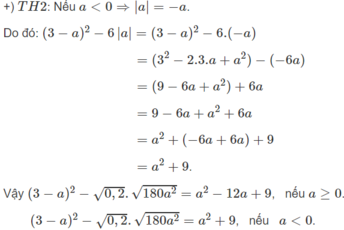
a/ \(\sqrt{\frac{2a}{3}}\cdot\sqrt{\frac{3a}{8}}\)
\(=\sqrt{\frac{2a}{3}\cdot\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\sqrt{\frac{a^2}{2^2}}=\sqrt{\left(\frac{a}{2}\right)^2}=\left|\frac{a}{2}\right|\)
mak ta có \(a\ge0\)
\(\Rightarrow\left|\frac{a}{2}\right|=\frac{a}{2}\)\(\Rightarrow\sqrt{\frac{2a}{3}}\cdot\sqrt{\frac{3a}{8}}=\frac{a}{2}\)
b/ \(\sqrt{13a}\cdot\sqrt{\frac{52}{a}}\)
\(=\sqrt{13a\cdot\frac{52}{a}}=\sqrt{\frac{13a\cdot52}{a}}=\sqrt{13\cdot52}=\sqrt{13\cdot13\cdot4}=\sqrt{13^2\cdot2^2}=\sqrt{\left(13\cdot2\right)^2}=13\cdot2=26\)
c/ \(\sqrt{5a}\cdot\sqrt{45}-3a\)
\(=\sqrt{5a\cdot45a}-3a=\sqrt{5a\cdot5a\cdot9}-3a\)
\(=\sqrt{5^2\cdot a^2\cdot3^2}-3a=\left|5\cdot a\cdot3\right|-3a\)
\(=15\left|a\right|-3a\)
Có \(a\ge0\Rightarrow\left|a\right|=a\)
\(\Rightarrow15\left|a\right|-3a=15a-3a=12a\)
\(\Rightarrow\sqrt{5a}\cdot\sqrt{45}-3a=12a\)
d/ \(\left(3-a\right)^2-\sqrt{0,2}\cdot\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{0,2\cdot180a^2}\)
\(=\left(3-a\right)^2-\sqrt{0,2\cdot9\cdot2\cdot10\cdot a^2}\)
\(=\left(3-a\right)^2-\sqrt{4\cdot9\cdot a^2}\)
\(=\left(3-a\right)^2-\sqrt{2^2\cdot3^2\cdot a^2}\)
\(=\left(3-a\right)^2-\left|2\cdot3\cdot a\right|\)
\(=\left(3-a\right)^2-6\left|a\right|=9-6a+a^2-6\left|a\right|\)
Chia làm 2 Trường Hợp:
+ TH1 : \(9-6a+a^2-6a=9-12a+a^2\left(a\ge0\right)\)
+ TH2 : \(9-6a+a^2-\left(-6a\right)=9+a^2\left(a< 0\right)\)
PT
1
18 tháng 8 2023
2b: \(=8\sqrt{2}-3\sqrt{2}-3\sqrt{2}-10\sqrt{2}=-8\sqrt{2}\)
3:
a: \(=\left(\sqrt{6a}+\dfrac{\sqrt{6a}}{3}+\sqrt{6a}\right):\sqrt{6a}\)
=1+1/3+1
=7/3
b: \(=\dfrac{2}{3a-1}\cdot\sqrt{3}\cdot a\cdot\left|3a-1\right|\)
\(=\dfrac{2\sqrt{3}\cdot a\left(1-3a\right)}{3a-1}=-2a\sqrt{3}\)