NL
9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
10 tháng 10 2021
Lời giải:
Gọi chiều cao của Lan là $a$ (cm)
Chiều cao trung bình của ba bạn:
$\frac{123+124+a}{3}=\frac{247+a}{3}$ (cm)
Theo bài ra ta có:
$a=\frac{247+a}{3}+3$
$a-3=\frac{247+a}{3}$
$3(a-3)=247+a$
$2a=256$
$a=128$ (cm)
Vậy Lan cao $128$ cm
NV
ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ
2
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
QN
0
giúp em với ạ em đang cần gấp ạ
3 tháng 7 2023
Bài 16
a) \(A=\dfrac{n+1}{n+2}\)
Gọi ƯCLN(n+1;n+2) là x ( \(x\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}\left(n+1\right)⋮x\\\left(n+2\right)⋮x\end{matrix}\right.\)
\(\Rightarrow\) \(\left(n+2\right)-\left(n+1\right)\) \(⋮x\)
\(\Rightarrow\) \(1\) \(⋮x\)
\(\Rightarrow\) x = 1 \(\Rightarrow\) ƯCLN(n+1;n+2)=1
Vậy A là phân số tối giản ( vì có ƯCLN = 1)
b) \(B=\dfrac{n+1}{3n+4}\)
Gọi ƯCLN(n+1;3n+4) là d ( \(d\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}n+1⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}3n+3⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) (3n+4)-(3n+3) chia hết cho d
\(\Rightarrow\) \(1⋮d\)
\(\Rightarrow\) d =1
Vậy B là phân số tối giản.
Mấy phần kia tương tự
3 tháng 7 2023
c: Gọi d=ƯCLN(3n+2;5n+3)
=>3n+2 chia hết cho d và 5n+3 chia hết cho d
=>15n+10 chia hết cho d và 15n+9 chia hết cho d
=>1 chia hết cho d
=>ƯCLN(3n+2;5n+3)=1
=>PSTG
d: Gọi d=ƯCLN(12n+1;30n+2)
=>12n+1 và 30n+2 đều chia hết cho d
=>60n+5 chia hết cho d và 60n+4 chia hết cho d
=>1 chia hết cho d
=>d=1
=>PSTG
giúp em với ạ em đang cần gấp ạ :(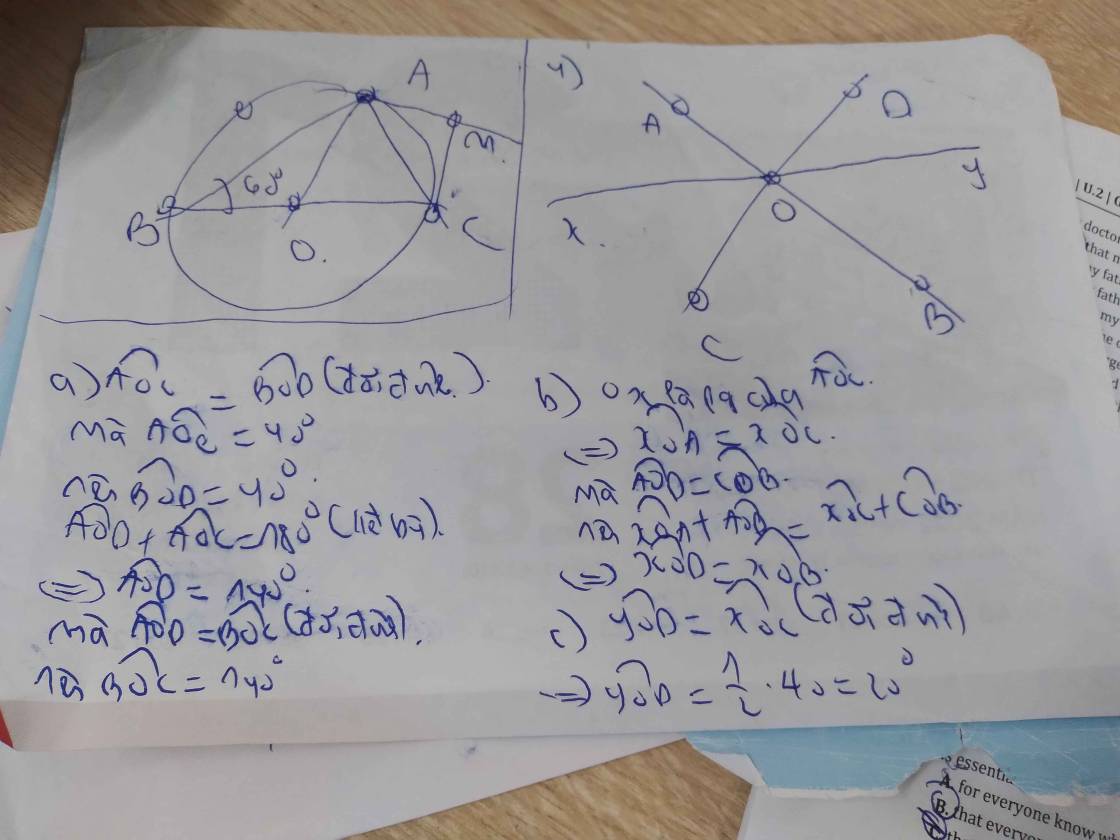
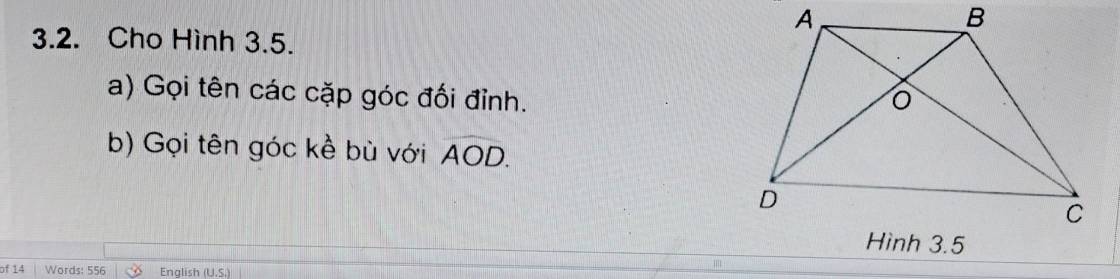chỉ em với ạ em đang cần gấp ạ
gạch chéo là chia ạ
Giải :
\(\left|-3,45\right|+\frac{1,5}{3}\)
\(=3,45+0,5\)
\(=3,95\)