
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có: 8x+8y+8z < 8x+9y+10z =100
=> x+y+z < 100/8 < 13
Ta lại có: x+y+z>11 nên 11< x+y+z < 13, nhưng x+y+z \(\in\)Z => x+y+z = 12
Ta có hệ: x+y+z = 12 (1)
=>8x+8y+8z=96 (2);
8x+9y+10z = 100 (3).
Trừ (3) cho (1),ta được:
y+2z = 4 (4)
Từ (4) suy ra z = 1 (vì nếu z ≥ 2 thì do y ≥ 1 => y+2z > 4,mâu thuẫn)
Với z = 1, thay vào (3), ta được:
\(y+2.1=4\Leftrightarrow y=4-2=2\)
Thay y = 2, z = 1 vào (1), ta được:
\(x+2+1=12\Leftrightarrow x=12-3=9\)
Vậy x = 9, y = 2, z = 1
Ta có:8x+8y+18z<8x+9y+10z=100\(\Rightarrow\)x+y+z<100/8<13
cùng với giả thiết ta có:11<x+y+z<13 nhưng x+y+z\(\in\)Z\(\Rightarrow\)x+y+z=12
Ta có:x+y+z=12(1);8x+9y+10z=100(2)
Nhân 2 vế của(1) với 8 rồi trừ vế của (2) cho (1) ta được y+2z=4(3)
Từ (3) suy ra z=1
Với z=1 ta được y=2;x=9
Vậy x=9;y=2;z=1

Từ GT \(\Leftrightarrow a>0;bc>0\)
\(BĐT\Leftrightarrow\dfrac{a^2}{3}+\left(b+c\right)^2-3bc-a\left(b+c\right)\ge0\\ \Leftrightarrow\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\ge0\)
Vì \(a^3>36\) nên
\(\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\\ >\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}+\dfrac{1}{4}=\left(\dfrac{b+c}{a}-\dfrac{1}{2}\right)^2\ge0\)

a) \(x^2+y^2=0\) ( 1 )
Ta có :
\(x^2\ge0\forall x\)
\(y^2\ge0\forall x\)
Để ( 1 ) = 0
\(\Rightarrow\hept{\begin{cases}x^2=0\\y^2=0\end{cases}}\)
\(\hept{\begin{cases}x=0\\y=0\end{cases}}\)
\(x^2+y^2=0\) với \(x=y=0\) là mệnh đề đúng
\(x^2+y^2=0\) với \(\orbr{\begin{cases}x\ne0\\y\ne0\end{cases}}\) là mệnh đề sai
b) \(x^2+y^2\ne0\) ( 2 )
Vì \(x^2\ge0\forall x\)
\(y^2\ge0\forall y\)
Nên \(x^2+y^2\ne0\Leftrightarrow\orbr{\begin{cases}x^2\ne0\\y^2\ne0\end{cases}}\)
\(\orbr{\begin{cases}x\ne0\\y\ne0\end{cases}}\)
\(x^2+y^2\ne0\) với \(\orbr{\begin{cases}x\ne0\\y\ne0\end{cases}}\) là mệnh đề đúng
\(x^2+y^2\ne0\) với \(\hept{\begin{cases}x=0\\y=0\end{cases}}\) là mệnh đề sai


Ta có:
\(\left(m^2+n^2\right)^2=\left(m^2-n^2\right)^2+\left(2mn\right)^2\left(1\right)\)
\(\Leftrightarrow m^4+2m^2n^2+n^4=m^4-2m^2n^2+n^4+4m^2n^2\)
\(\Leftrightarrow m^4+2m^2n^2+n^4=m^4+2m^2n^2+n^4\) (luôn đúng)
Lạ có: \(a=m^2+n^2;b=m^2-n^2;c=2mn\)
Nên từ \(\left(1\right)\) suy ra \(a^2=b^2+c^2\)
Đúng theo định lý Py-ta-go đảo
Hay a,b,c là cạnh một tam giác vuông

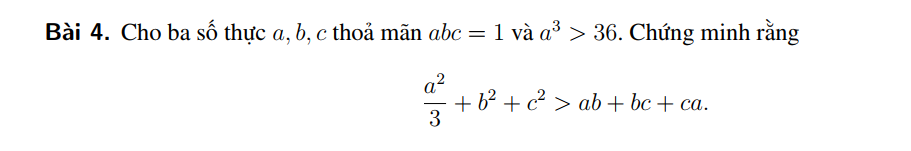


ko đăng linh tinh nữa nha bạn