Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt biểu thức là A
\(4xA=\frac{4}{2x4x6}+\frac{4}{4x6x8}+\frac{4}{6x8x10}+\frac{4}{8x10x12}+...+\frac{4}{94x96x98}+\frac{4}{96x98x100}\)
\(4xA=\frac{6-2}{2x4x6}+\frac{8-4}{4x6x8}+\frac{10-6}{6x8x10}+\frac{12-8}{8x10x12}+...+\frac{98-94}{94x96x98}+\frac{100-96}{96x98x100}\)
\(4xA=\frac{1}{2x4}-\frac{1}{4x6}+\frac{1}{4x6}-\frac{1}{6x8}+\frac{1}{6x8}-\frac{1}{8x10}+...+\frac{1}{94x96}-\frac{1}{96x98}+\frac{1}{96x98}-\frac{1}{98x100}\)
\(4xA=\frac{1}{2x4}-\frac{1}{98x100}=\frac{49x50-1}{98x100}\Rightarrow A=\frac{49x50-1}{4x98x100}\)

A = \(\dfrac{1\times3\times5+2\times6\times10+3\times9\times15}{3\times5\times12+6\times10\times24+9\times15\times36}\)
A = \(\dfrac{1\times3\times5+2\times6\times10+3\times9\times15}{3\times5\times12+6\times10\times2\times12+9\times15\times3\times12}\)
A = \(\dfrac{1\times3\times5+2\times6\times10+3\times9\times15}{12\times\left(1\times3\times5+6\times10\times2+9\times15\times3\right)}\)
A = \(\dfrac{1\times3\times5+2\times6\times10+3\times9\times15}{12\times\left(1\times3\times5+2\times6\times10+3\times9\times15\right)}\)
A = \(\dfrac{1}{12}\)
A = 1×3×5+2×6×10+3×9×153×5×12+6×10×24+9×15×36
A = 1×3×5+2×6×10+3×9×153×5×12+6×10×2×12+9×15×3×12
A = 1×3×5+2×6×10+3×9×1512×(1×3×5+6×10×2+9×15×3)
A = 1×3×5+2×6×10+3×9×1512×(1×3×5+2×6×10+3×9×15)
A = 112

1\(\times\)3\(\times\)5\(\times\)...\(\times\)97\(\times\)99
= \(\overline{...5}\)
Chữ số tận cùng của tích trên là 5 vì tích của thừa số 5 với các thừa số lẻ có tận cùng là 5

\(A=9\left(\dfrac{4}{1\cdot3\cdot5}+\dfrac{4}{3\cdot5\cdot7}+...+\dfrac{4}{25\cdot27\cdot29}\right)\)
\(=9\left(\dfrac{1}{1\cdot3}-\dfrac{1}{3\cdot5}+\dfrac{1}{3\cdot5}-\dfrac{1}{5\cdot7}+...+\dfrac{1}{25\cdot27}-\dfrac{1}{27\cdot29}\right)\)
\(=9\left(\dfrac{1}{3}-\dfrac{1}{783}\right)=\dfrac{260}{87}\)


\(\frac{4}{1x3x5}+\frac{4}{3x5x7}+...+\frac{4}{9x11x13}\)
\(=\frac{1}{1x3}-\frac{1}{3x5}+\frac{1}{3x5}-...+\frac{1}{9x11}-\frac{1}{11x13}\)
\(=\frac{1}{3}-\frac{1}{143}\)
\(=\frac{140}{429}\)

\(\dfrac{4}{1\times3\times5}+\dfrac{4}{3\times5\times7}+\dfrac{4}{5\times7\times9}+\dfrac{4}{7\times9\times11}\)
=\(\dfrac{5-1}{1\times3\times5}+\dfrac{7-3}{3\times5\times7}+\dfrac{9-5}{5\times7\times9}+\dfrac{11-7}{7\times9\times11}\)
=\(\dfrac{1}{1\times3}-\dfrac{1}{3\times5}+\dfrac{1}{3\times5}-\dfrac{1}{5\times7}+...+\dfrac{1}{9\times11}-\dfrac{1}{11\times13}\)
=\(\dfrac{1}{3}-\dfrac{1}{143}=\dfrac{140}{429}\)


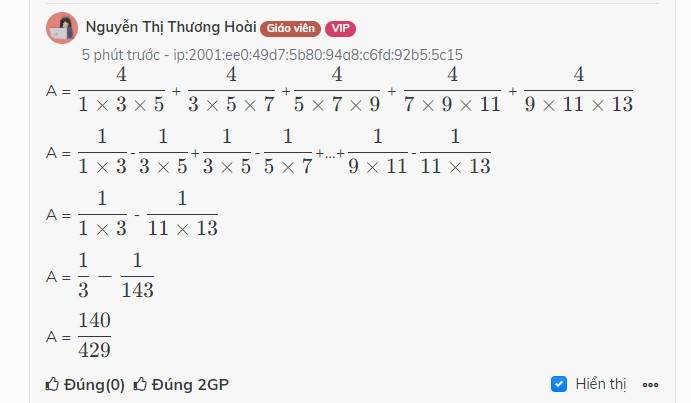
A = \(\dfrac{4}{1\times3\times5}\) + \(\dfrac{4}{3\times5\times7}\) +\(\dfrac{4}{5\times7\times9}\) + \(\dfrac{4}{7\times9\times11}\) + \(\dfrac{4}{9\times11\times13}\)
A = \(\dfrac{1}{1\times3}\)-\(\dfrac{1}{3\times5}\)+\(\dfrac{1}{3\times5}\)-\(\dfrac{1}{5\times7}\)+...+\(\dfrac{1}{9\times11}\)-\(\dfrac{1}{11\times13}\)
A = \(\dfrac{1}{1\times3}\) - \(\dfrac{1}{11\times13}\)
A = \(\dfrac{1}{3}-\dfrac{1}{143}\)
A = \(\dfrac{140}{429}\)
Bài 2:
A = \(\dfrac{1991}{1990}\) x \(\dfrac{1992}{1991}\) x \(\dfrac{1993}{1992}\) x \(\dfrac{1994}{1993}\) x \(\dfrac{1995}{997}\)
A = \(\dfrac{1994\times1995}{1990\times997}\)
A = \(\dfrac{997\times2\times5\times399}{5\times2\times199\times997}\)
A = \(\dfrac{399}{199}\)