Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
O 8 -8 4 M N P x
Pha ban đầu bằng 0 nên véc tơ quay xuất phát tại M.
Khi vật qua x = 4 cm thì véc tơ quay quay đến N hoặc P.
Cho véc tơ quay xuất phát ở M quay ngược chiều kim đồng hồ. Khi nó quay được 1004 vòng thì nó qua N và P là 2008 lần, lần cuối cùng nó quay từ M đến N.
Vậy thời gian tương ứng: \(t=1004T+\dfrac{60}{360}T=(1004+\dfrac{1}{6}).\dfrac{2\pi}{10\pi}=200,83(s) \)

Đáp án A
Phương pháp: Sử dụng vòng tròn lượng giác
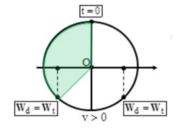
Định luật bảo toàn cơ năng W = Wđ + Wt
Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là T/4
Cách giải:
Wđ + Wt tại những vị trí x = ± A 2 sau những khoảng thời gian cách đều là T/4
Một chu kỳ có 2 lần Wđ + Wt theo chiều (+) ta có 2017 2 = 1008 dư 1 => ∆ t = 1008 T + t 1
Dựa vào đường tròn lượng giác ta có
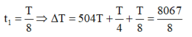

Mỗi câu hỏi bạn nên hỏi 1 bài thôi để tiện trao đổi nhé.
Biểu diễn dao động bằng véc tơ quay ta có:
M x 2 1 O N
Để vật qua li độ 1 cm theo chiều dương thì véc tơ quay qua N.
Trong giây đầu tiên, véc tơ quay đã quay 1 góc là: \(5\pi\), ứng với 2,5 vòng quay.
Xuất phát từ M ta thấy véc tơ quay quay đc 2,5 vòng thì nó qua N 3 lần do vậy trong giây đầu tiên, vật qua li độ 1cm theo chiều dương 3 lần.
Bạn xem thêm lí thuyết phần này ở đây nhé
Phương pháp véc tơ quay và ứng dụng | Học trực tuyến
Bài 1 :
T = 2π / ω = 0.4 s
Vật thực hiện được 2 chu kì và chuyển động thêm trong 0.2 s (T/2 ) nữa
1 chu kì vật qua vị trí có li độ x=2cm theo chiều dương được "1 " lần
⇒ 2 ________________________________________... lần
phần lẻ 0.2s (T/2) , (góc quét là π ) (tức là chất điểm CĐ tròn đều đến vị trí ban đầu và góc bán kính quét thêm π (rad) nữa, vị trí lúc nầy:
x = 1 + 2cos(-π/2 + π ) = 1, (vận tốc dương) vật qua vị trí có li độ x=2cm theo chiều dương thêm 1 lần nữa
(từ VT ban đầu (vị tri +1 cm ) –> biên dương , về vị trí có ly độ x = +1 cm
do đó trong giây đầu tiên kể từ lúc t=0 vật qua vị trí có li độ x=2cm theo chiều dương được 3 lần
Chọn A

Chọn đáp án B
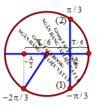
+ Chu kì T = 2 π ω = 1 s
+ Từ vòng tròn lượng giác ta thấy:
• Lần 1: Vật đến x = A 2 là t 01 = T 6
• Lần 2: t 02 = T 6 + T 6 + T 6 = T 2
……
• Lần 231 = 2.115 + 1 là: t 231 = n T + t 01 = 115 T + T 6 = 691 6 s
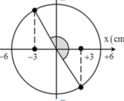

1/ Đề bài bài 1 ko được chắt chẽ lắm, phải nói là tính thời gian kể từ lúc xuất phát đến lúc có li độ x=-1cm mà lúc này, vận tốc của vật là âm. Tương tự với câu b
a/ Vẽ đường tròn, đầu tiền vật đi từ vị trí -pi/6 đến biên độ dương là quay được pi/6, sau đó từ từ biên độ dương đến VTCB quay một góc pi/2, từ VTCB đến điểm có li độ x=-1cm thì quay một góc pi/6.
Vậy vật phải quay một góc là \(\varphi=\dfrac{\pi}{6}+\dfrac{\pi}{2}+\dfrac{\pi}{6}=\dfrac{5\pi}{6}\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{\dfrac{5}{6}\pi}{2\pi}=\dfrac{5}{12}\left(s\right)\)
b/ Nối tiếp câu a, lúc này vật đang ở vị trí có li độ x=-1cm, để đến biên độ âm thì phải quay góc pi/3, từ biên âm đến vị trí có li độ x=-1cm mà lúc này vận tốc vật là dương thì phải quay thêm pi/3 nữa.
Vậy vật phải quay:
\(\varphi=\dfrac{\pi}{6}+\dfrac{\pi}{2}+\dfrac{\pi}{2}+\dfrac{\pi}{3}=\dfrac{3}{2}\pi\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{\dfrac{3}{2}\pi}{2\pi}=\dfrac{3}{4}\left(s\right)\)
2/ Qua VTCB 5 lần, nghĩa là quay được 2 vòng, và thêm một góc là pi/2 nữa
Vậy vật quay được góc là:
\(\varphi=2\pi+\dfrac{\pi}{2}=\dfrac{5}{2}\pi\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{\dfrac{5}{2}\pi}{2\pi}=\dfrac{5}{4}\left(s\right)\)