Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều
\(\Rightarrow S_{ABCD}=2S_{ABC}=2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{2}\)
Gọi O là giao điểm 2 đường chéo \(\Rightarrow SO\perp AC\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{AC\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{a^3}{4}\)
2.
Gọi M là trung điểm AB \(\Rightarrow SM\perp AB\Rightarrow SM\perp\left(ABCD\right)\)
\(SM=\dfrac{AB\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam giác vuông MBC:
\(CM^2=BM^2+BC^2=\left(\dfrac{AB}{2}\right)^2+\left(2AB\right)^2=\dfrac{17AB^2}{4}\)
Áp dụng định lý Pitago cho tam giác vuông SMC:
\(SC^2=SM^2+CM^2\Leftrightarrow5a^2=\dfrac{3AB^2}{4}+\dfrac{17AB^2}{4}=5AB^2\)
\(\Rightarrow AB=a\Rightarrow\left\{{}\begin{matrix}AD=2a\\SM=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
\(V=\dfrac{1}{3}.SM.AB.AD=\dfrac{a^3\sqrt{3}}{3}\)

Đáp án D.
Phương pháp giải: Dựng hình, dựa vào tam giác cân để xác định các yếu tố vuông góc
Lời giải: Với hình chóp tam giác đều S.ABC thì: góc giữa các cạnh bên và mặt đáy bằng nhau, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trọng tâm tam giác ABC, hai cạnh đối diện vuông góc với nhau.
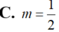

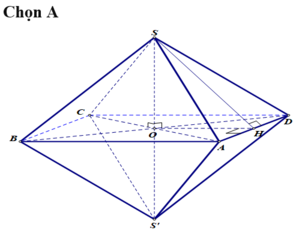





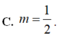
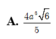

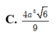
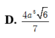

hai góc bằng nhau thì hai góc đó đối đỉnh
mọi số chia hết cho 3 thì chia hết cho 6
mọi tứ giác có 2 đường chéo bằng nhau thì tứ giác đó là hình chữ nhật