Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\Leftrightarrow20x^2-12x+15x+5< 10x\left(2x+1\right)-30\)
\(\Leftrightarrow20x^2+3x+5< 20x^2+10x-30\)
=>3x+5<10x-30
=>-7x<-35
hay x>5
b: \(\Leftrightarrow4\left(5x-20\right)-6\left(2x^2+x\right)>4x\left(1-3x\right)-15x\)
\(\Leftrightarrow20x-80-12x^2-6x>4x-12x^2-15x\)
=>14x-80>-11x
=>25x>80
hay x>16/5

a: =>2x^2+8x-3x-12<2x^2+2
=>5x<14
=>x<14/5
b: =>\(\dfrac{9x-3-\left(5x+1\right)\left(x-2\right)}{3\left(x-2\right)}-4>0\)
=>\(\dfrac{9x-3-5x^2+10x-x+2-12\left(x-2\right)}{3\left(x-2\right)}>0\)
=>\(\dfrac{-5x^2+18x-1-12x+24}{3\left(x-2\right)}>0\)
=>\(\dfrac{-5x^2+6x+23}{x-2}>0\)
TH1: x-2>0 và -5x^2+6x+23>0
=>x>2 và \(\dfrac{3-2\sqrt{31}}{5}< x< \dfrac{3+2\sqrt{31}}{5}\)
=>\(2< x< \dfrac{3+2\sqrt{31}}{5}\)
TH2: x-2<0 và -5x^2+6x+23<0
=>x<2 và \(\left[{}\begin{matrix}x< \dfrac{3-2\sqrt{31}}{5}\\x>\dfrac{3+2\sqrt{31}}{5}\end{matrix}\right.\)
=>\(x< \dfrac{3-2\sqrt{31}}{5}\)

Bài 4 :
24 phút = \(\dfrac{24}{60} = \dfrac{2}{5}\) giờ
Gọi thời gian dự định đi từ A đến B là x(giờ) ; x > 0
Suy ra quãng đường AB là 36x(km)
Khi vận tốc sau khi giảm là 36 -6 = 30(km/h)
Vì giảm vận tốc nên thời gian đi hết AB là x + \(\dfrac{2}{5}\)(giờ)
Ta có phương trình:
\(36x = 30(x + \dfrac{2}{5})\\ \Leftrightarrow x = 2\)
Vậy quãng đường AB dài 36.2 = 72(km)

a: Ta có: \(3x-\left(3x+2\right)=x+3\)
\(\Leftrightarrow x+3=-2\)
hay x=-5
b: Ta có: \(\dfrac{5x-1}{4}+\dfrac{2x-1}{3}=\dfrac{3x}{2}\)
\(\Leftrightarrow15x-3+8x-4=18x\)
\(\Leftrightarrow5x=7\)
hay \(x=\dfrac{7}{5}\)

g.\(\dfrac{1-3x}{6}+x-1=\dfrac{x+2}{2}\)
\(\Leftrightarrow\dfrac{\left(1-3x\right)+6\left(x-1\right)}{6}=\dfrac{3\left(x+2\right)}{6}\)
\(\Leftrightarrow\left(1-3x\right)+6\left(x-1\right)=3\left(x+2\right)\)
\(\Leftrightarrow1-3x+6x-6=3x+6\)
\(\Leftrightarrow-5=6\left(vô.lí\right)\)
Vậy pt vô nghiệm
h.\(\dfrac{3\left(2x+1\right)}{4}-5-\dfrac{3x+2}{10}=\dfrac{2\left(3x-1\right)}{5}\)
\(\Leftrightarrow\dfrac{15\left(2x+1\right)-100-2\left(3x+2\right)}{20}=\dfrac{8\left(3x-1\right)}{20}\)
\(\Leftrightarrow15\left(2x+1\right)-100-2\left(3x+2\right)=8\left(3x-1\right)\)
\(\Leftrightarrow30x+15-100-6x-4=24x-8\)
\(\Leftrightarrow-89=-8\left(vô.lí\right)\)
Vậy pt vô nghiệm

`a,` \(\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)
`<=> (5(5x+2))/30 - (10(8x-1))/30 = (6(4x+2))/30 - (5.30)/30`
`<=> 5(5x+2) - 10(8x-1) =6(4x+2) - 5.30`
`<=> 25x + 10 - 80x + 10 = 24x+12 - 150`
`<=> -55x +20 = 24x-138`
`<=> -55x -24x=-138-20`
`<=>-79x=-158`
`<=> x=2`
Vậy pt có nghiệm `x=2`
`b,` \(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\)
ĐKXĐ : \(\left\{{}\begin{matrix}x-2\ne0\\x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne0\end{matrix}\right.\)
Ta có : `(x+2)/(x-2) -1/x = 2/(x(x-2))`
`<=> (x(x+2))/(x(x-2)) - (x-2)/(x(x-2)) = 2/(x(x-2))`
`=> x^2 +2x - x +2 = 2`
`<=> x^2 + x =0`
`<=>x(x+1)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(l\right)\\x=-1\end{matrix}\right.\)
Vậy pt có nghiệm `x=-1`
`c,2x^3 + 6x^2 =x^2 +3x`
`<=> 2x^3 + 6x^2 -x^2 -3x=0`
`<=> 2x^3 + 5x^2 -3x=0`
`->` Đề có sai ko ạ ?
`d,` \(\left|x-4\right|+3x=5\) `(1)`
Thường hợp `1` : `x-4 >= 0<=> x >=0` thì phương trình `(1)` thở thành :
`x-4 = 5-3x`
`<=> x+3x=5+4`
`<=> 4x=9`
`<=> x= 9/4 (t//m)`
Trường hợp `2` : `x-4< 0<=> x<0` thì phương trình `(1)` trở thành :
`-(x-4) =5-3x`
`<=> -x +4=5-3x`
`<=> -x+3x=5-4`
`<=> 2x =1`
`<=>x=1/2 ( kt//m)`
Vậy phương trình có nghiệm `x=9/4`

a:Sửa đề: \(\dfrac{3}{5x-1}+\dfrac{2}{3-x}=\dfrac{4}{\left(1-5x\right)\left(x-3\right)}\)
=>3x-9-10x+2=-4
=>-7x-7=-4
=>-7x=3
=>x=-3/7
b: =>\(\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8x}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
=>\(2\left(5-x\right)+7\left(x-2\right)=4\left(x-1\right)+x\)
=>10-2x+7x-14=4x-4+x
=>5x-4=5x-4
=>0x=0(luôn đúng)
Vậy: S=R\{0;2}


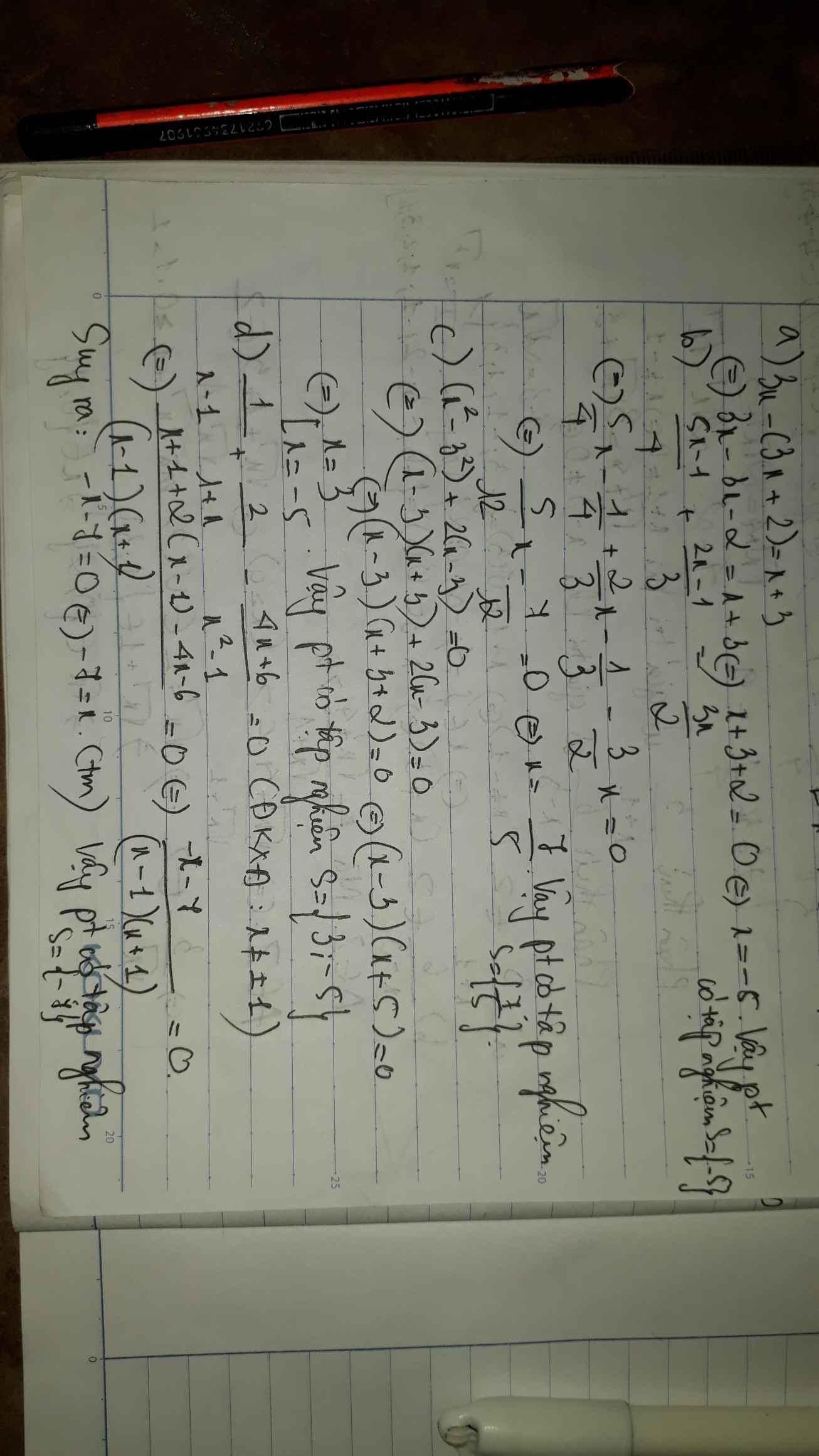
\(\left(\dfrac{3x}{2}-1\right)^2-\dfrac{x}{2}\cdot\left(\dfrac{5x}{2}-2\right)\le0\) (1)
\(\Leftrightarrow\dfrac{9x^2}{4}-\dfrac{6x}{2}+1-\dfrac{x}{2}\cdot\dfrac{5x-4}{2}\le0\)
\(\Leftrightarrow\dfrac{9x^2}{4}-3x+1-\dfrac{x\left(5x-4\right)}{4}\le0\)
\(\Leftrightarrow\dfrac{9x^2}{4}-3x+1-\dfrac{5x^2-4x}{4}\le0\)
\(\Leftrightarrow9x^2-12x+4-\left(5x^2-4x\right)\le0\)
\(\Leftrightarrow9x^2-12x+4-5x^2+4x\le0\)
\(\Leftrightarrow4x^2-8x+4\le0\)
\(\Leftrightarrow x^2-2x+1\le0\)
\(\Leftrightarrow\left(x-1\right)^2\le0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x=1\)
Vậy tập nghiệm phương trình (1) là \(S=\left\{1\right\}\)