
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT \(\sqrt{a}+\sqrt{b}\ge\sqrt{a+b}\) ta có:
\(VT=\sqrt{10-x}+\sqrt{x+6}\)
\(\ge\sqrt{10-x+x+6}=\sqrt{16}=4\)
Và \(VP=-x^2-12x-32=-x^2-12x-36+4\)
\(=-\left(x^2+12x+36\right)+4\)\(=-\left(x+6\right)^2+4\le4\)
\(\Rightarrow VT\ge VP=4\) xảy ra khi \(VT=VP=4\)
\(\Rightarrow-\left(x+6\right)^2+4=4\Rightarrow x=-6\)

Ta có: ∆ ’ = - 6 2 -1.32 = 36 - 32 = 4 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Giải ra ta được x 1 =4, x 2 =8

Đặt \(\sqrt{x};\sqrt{y};\sqrt{z}\rightarrow a,b,c\), ta có : \(a+b+c=1\)
Tìm min của \(A=\frac{ab}{\sqrt{5a^2+32ab+12b^2}}+\frac{bc}{\sqrt{5b^2+32bc+12c^2}}+\frac{ca}{\sqrt{5c^2+32ca+12a^2}}\)
đến đây thấy giống giống bài bất của HN năm nào ấy nhỉ ?

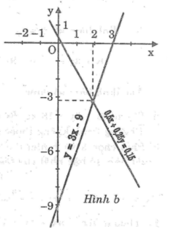
*Ta có: 0,5x + 0,25y = 0,15 ⇔ y = -2x + 0,6
Cho x = 0 thì y = 0,6 ⇒ (0; 0,6)
Cho y = 0 thì x = 0,3 ⇒ (0,3; 0)
*Ta có: 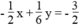 ⇔ y = 3x – 9
⇔ y = 3x – 9
Cho x = 0 thì y = -9 ⇒ (0; -9)
Cho y = 0 thì x = 3 ⇒ (3; 0)
Hoành độ giao điểm của hai đường thẳng:
-2x + 0,6 = 3x – 9 ⇔ 5x = 9,6 ⇔ x = 1,92
Tung độ giao điểm của hai đường thẳng:
y = 3.1,92 – 9 = -3,24
Vậy tọa độ giao điểm của hai đường thẳng là (1,92; -3,24)
Đồ thị:

a. Ta có: Δ’ = (-3)2 -1.8=9 -8 =1 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Giải ra ta được x1 =2, x2 =4
b. Ta có: Δ’ = (-6)2 -1.32 = 36 - 32 = 4 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Giải ra ta được x1 =4,x2 =8
c. Ta có: Δ’ = 32 -1.8=9 -8 =1 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Giải ra ta được x1 =-2, x2 =-4
d. Ta có: Δ = (-3)2 -4.1.(-10)=9 +40 =49 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
Giải ra ta được x1 =-2, x2 =5
e. Ta có: Δ = 32 -4.1.(-10)=9 +40 =49 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:

Câu 1:
\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=3\)(1)
Trường hợp 1: x<1
(1) trở thành 1-x+2-x=3
=>3-2x=3
=>x=0(nhận)
Trường hợp 2: 1<=x<2
(1) trở thành x-1+2-x=3
=>1=3(loại)
Trường hợp 3: x>=2
(1) trở thành x-1+x-2=3
=>2x-3=3
=>2x=6
hay x=3(nhận)
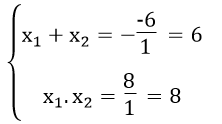
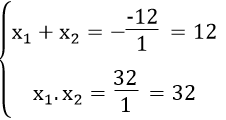
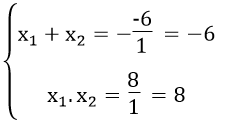
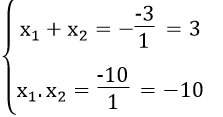
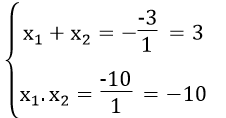
\(mx^2+2\left(m-2\right)x+m-1=0\) ( đkxđ : m khác 0 )
PT có 2 nghiệm phân biệt
\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\x_1x_2=\frac{m-1}{m}\\x_1+x_2=\frac{-\left(2m-4\right)}{m}\end{cases}\Leftrightarrow\hept{\begin{cases}\left(m-2\right)^2-\left(m-1\right)m>0\left(1\right)\\x_1x_2=\frac{m-1}{m}\\x_1+x_2=\frac{-\left(2m-4\right)}{m}\end{cases}}}\)
giải ( 1 ) ta được : \(m< \frac{4}{3}\) ( * )
PT có 2 nghiệm phân biệt nhỏ hơn 1 \(\Leftrightarrow\hept{\begin{cases}x_1< 1\\x_2< 1\end{cases}}\Leftrightarrow\hept{\begin{cases}x_1-1< 0\\x_2-1< 0\end{cases}}\)
\(\Rightarrow\left(x_1-1\right)\left(x_2-1\right)>0\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1>0\Leftrightarrow\frac{m-1}{m}+\frac{2m-4}{m}+1>0\)
\(\Leftrightarrow\frac{4m-5}{m}>0\left(2\right)\)
giải ( 2 ) ta được : \(\orbr{\begin{cases}m>\frac{5}{4}\\m< 0\end{cases}}\) ( ** )
từ ( * ) và ( ** ) , kết hợp điều kiện ta có : \(\orbr{\begin{cases}m< 0\\\frac{5}{4}< m< \frac{4}{3}\end{cases}}\)
bạn NaNis ơi. mình làm xong bạn sửa đề là sao. lỡ mọi người hiểu lầm thì sao