
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi chiều rộng của hình chữ nhật là a(0<a<1005)
=>chiều dài của hình chữ nhật là 1005-a
theo đề bài ta có pt:
a(1005-a)+13300=(a+10)(1005-a+20)
<=>-a^2+1005a+13300=-a^2+1025a-10a+102...
<=>10a=3050
<=>a=305
=>rộng=305:dài=700
mình lớp 5 mong các bạn tích thật nhiều và luôn
Gọi chiều dài ban đầu hcn là x (0<x<2010)
Gọi chiều rộng ban đầu hcn là y (0<y<x)
=>diện tích hcn ban đầu là: xy (cm2)
do hcn ban đầu có chu vi =2010cm nên ta có pt:
2(x+y)=2010 <=> x+y=1005 (1)
Khi tăng chiều dài thêm 20cm thì chiều dài mới là: (x+20) cm
và tăng chiều rộng thêm 10cm thì chiều rộng mới là (y+10) cm
Do đó diện tích hcn ban đâu tăng lên 13300 cm2
=>ta có pt: ( x+20)(y+10)=xy+13300 <=> x+2y=1310 (2)
từ (1)và (2) ta có hệ:
x+y=1005
x+2y=1310
Giải hệ pt ta đc: x=700; y=305
Vậy chiều dài ban đầu của hcn là 700 cm
chiều rộng ban đầu là 305 cm




b: Xét ΔDEF vuông tại D có DK là đường cao
nên \(DF^2=EF\cdot KF\)

Kb luôn nhé. Chắc là bạn mới lập nick à. Mk nói thật Mk hết lượt kb roài

7:
a: ĐKXĐ: x>=0; x<>1
\(D=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\)
\(=\dfrac{1}{2\left(\sqrt{x}-1\right)}-\dfrac{1}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)
b: Khi x=4/9 thì \(D=\dfrac{-1}{\dfrac{2}{3}+1}=-1:\dfrac{5}{3}=-\dfrac{3}{5}\)
c: |D|=1/3
=>D=-1/3 hoặc D=1/3
=>\(\left[{}\begin{matrix}\dfrac{-1}{\sqrt{x}+1}=\dfrac{-1}{3}\\\dfrac{-1}{\sqrt{x}+1}=\dfrac{1}{3}\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}+1=3\)
=>\(\sqrt{x}=2\)
=>x=4
6:
a: \(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}-x+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\)
\(=\dfrac{3\left(\sqrt{x}+3\right)}{3+\sqrt{x}}\cdot\dfrac{-\sqrt{x}}{2\sqrt{x}+4}=\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
b: C<-1
=>C+1<0
=>\(\dfrac{-3\sqrt{x}+2\sqrt{x}+4}{2\sqrt{x}+4}< 0\)
=>\(-\sqrt{x}+4< 0\)
=>\(-\sqrt{x}< -4\)
=>\(\sqrt{x}>4\)
=>x>16
\(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\\ =\dfrac{3\sqrt{x}-x+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{3\left(\sqrt{x}+3\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
Để `C < -1` Ta có :
\(\dfrac{-3}{2\sqrt{x}+4}< -1\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+1< 0\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+\dfrac{2\sqrt{x}+4}{2\sqrt{x}+4}< 0\\ \Leftrightarrow-3+2\sqrt{x}+4< 0\\ \Leftrightarrow2\sqrt{x}+1< 0\\ \Leftrightarrow2\sqrt{x}< -1\\ \Leftrightarrow\sqrt{x}< -\dfrac{1}{2}\\ \Leftrightarrow x< \dfrac{1}{4}\)
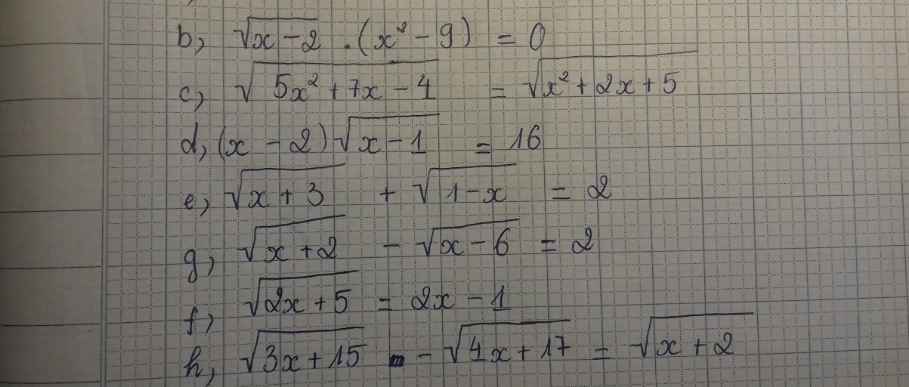
 cho mik lời giải nữa nhá thanks
cho mik lời giải nữa nhá thanks
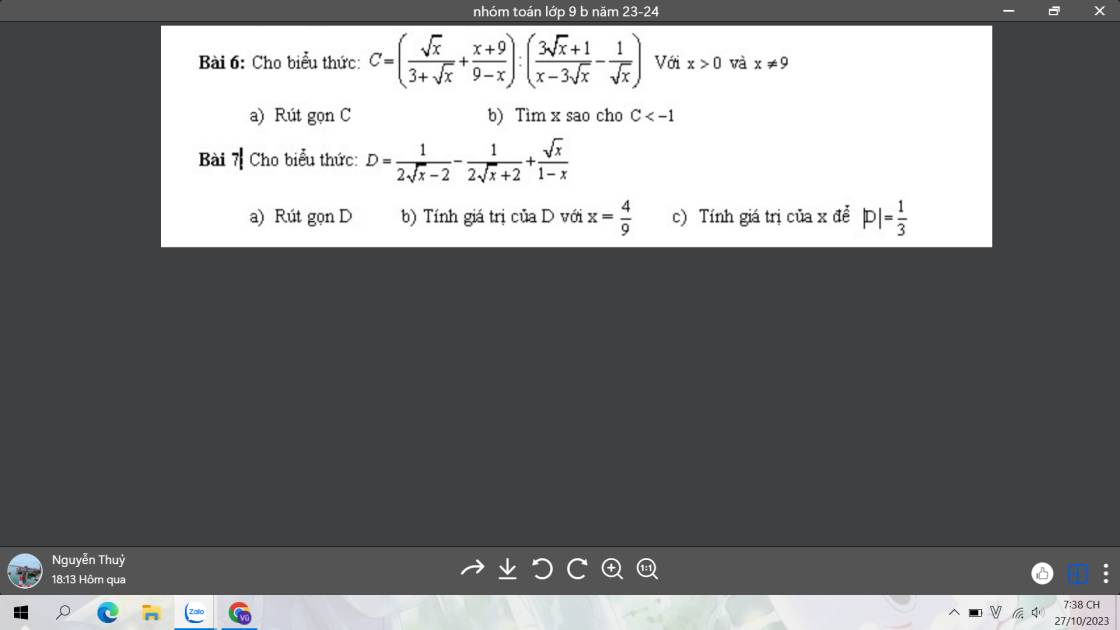 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp