Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tứ giác BCEF có
^CEB = ^CFB = 900
mà 2 góc này kề, cùng nhìn cạnh BC
Vậy tứ giác BCEF là tứ giác nt 1 đường tròn
b, Xét tứ giác AEHF có
^HEA = ^HFA = 900
Vậy tứ giác AEHF là tứ giác nt 1 đường tròn
c, Ta có ^AMN = ^ACN ( góc nt chắn cung AN )
^ANM = ^MBA ( góc nt chắn cung MA )
mà ^ACN = ^MBA ( tứ giác BCEF nt và 2 góc cùng nhìn cung CF )
=> ^AMN = ^ANM Vậy tam giác AMN cân tại A
=> AN = AM
d, Ta có : ^CBM = ^CFE ( góc nt chắn cung CE của tứ giác BCEF )
mặt khác : ^CNM = ^CBM ( góc nt chắn cung CM )
=> ^CFE = ^CNM, mà 2 góc này ở vị trí đồng vị )
=> MN // EF
e, Ta có AO là đường cao tam giác MAN
mà MN // EF ; AO vuông MN => AO vuông EF

a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó:BCEF là tứ giác nội tiếp
b: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp

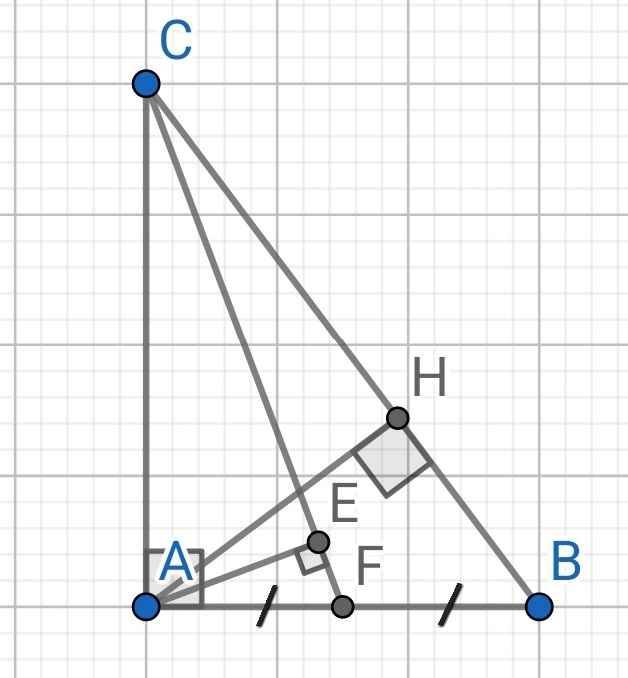 a) ∆ABC vuông tại A có AH là đường cao
a) ∆ABC vuông tại A có AH là đường cao
⇒ AH² = BH . CH
= 9 . 16
= 144
⇒ AH = 12 (cm)
BC = BH + CH
= 9 + 16
= 25 (cm)
∆ABC vuông tại A có AH là đường cao
⇒ AB² = BH . BC
= 9 . 25
= 225
⇒ AB = 15 (cm)
AC² = CH . BC
= 16 . 25
= 400
⇒ AC = 20 (cm)
b) Do F là trung điểm AB
⇒ AF = AB : 2 = 15 : 2 = 7,5 (cm)
∆ACF vuông tại A
⇒ tanAFC = AC/AF = 20/7,5 = 8,3
⇒ ∠AFC ≈ 69⁰
c) Do AE ⊥ CF (gt)
⇒ AE là đường cao của ∆ACF
∆ACF vuông tại C có CE là đường cao
⇒ AC² = CE.CF (1)
∆ABC vuông tại A có AH là đường cao
⇒ AC² = BC.CH (2)
Từ (1) và (2) suy ra:
CE.CF = BC.CH

Xin lỗi em, lúc nãy thầy vẽ sai hình nên cho rằng em post sai đề. Đề hoàn toàn đúng và cách giải như sau;
Gọi N là trung điểm BC thì A,O,K,N thẳng hàng (do O là trọng tâm). Ta có NM là đường trung bình nên \(MN\parallel AH\to MN=\frac{1}{2}CH=\frac{3}{4}CO\to\frac{NK}{KO}=\frac{3}{4}\to KO=\frac{4}{7}ON=\frac{2}{7}AO\to AK=\frac{9}{7}AO.\).
Theo định lý Pi-ta-to \(AO^2=AH^2+OH^2=\left(\frac{\sqrt{3}}{2}\right)^2+\left(\frac{\sqrt{2}}{3}\right)^2=\frac{3}{4}+\frac{2}{9}=\frac{35}{36}\to AO=\frac{\sqrt{35}}{6}\to AK=\frac{3\sqrt{35}}{14}\) (1)
Mặt khác \(\frac{KM}{KC}=\frac{MN}{CO}=\frac{3}{4}\to KM=\frac{3}{7}CM.\) Mà \(CM^2=CH^2+HM^2=2+\left(\frac{\sqrt{3}}{4}\right)^2=2+\frac{3}{16}=\frac{35}{16}\to CM=\frac{\sqrt{35}}{4}\to KM=\frac{3\sqrt{35}}{28}\) (2)
Từ (1),(2) trên suy ra \(\frac{KM}{AK}=\frac{1}{2}=\frac{HM}{HB}=\frac{HM}{HA}\to\) \(KH\) là phân giác của góc \(AKM.\)