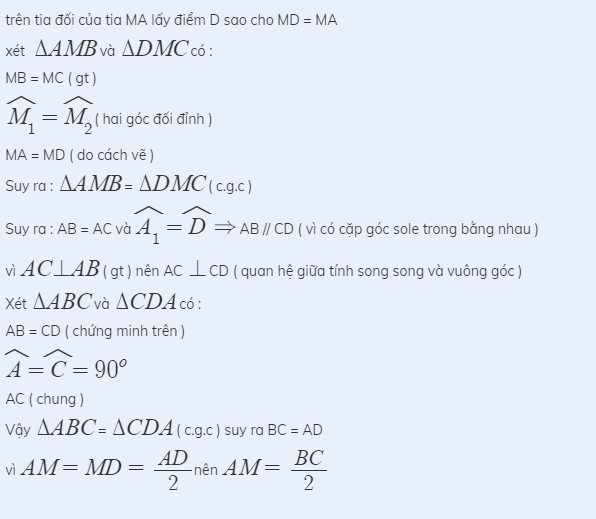Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông.
Đảo:
Tam giác có bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại là tam giác vuông.
Có thể ko chính xác từng chữ (do lười học bài cũ), bạn thông cảm nhé ^^!
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
Đảo:
Trong một tam giác, nếu có bình phương một cạnh bẳng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông
Nếu mình nhớ ko nhầm thì hình như hai định lý được phát biểu như thế này. Nếu có gì sai xin các bạn thông cảm

Pain Thiên Đạoko bt đừng trả lời ok mà ai chẳng bt là có pytago đảo cód đứa sống ngoài ngân hà ms ko bt

giả sử tam giác ABC có 2 đường trung tuyến BM và CN gặp nhau ở G
=> G là trong tâm của tam giác
-> GB=BM ; GC = CN
mà BM=CN (gt) nên GB = GC
=> tam giác GBC cân tại G
Do đó tam giác BCN=tam giác CBM vì:
BC là cạnh chung
CN = BM (gt)
=> tam giác ABC cân tại A
xét tam giác ABD và ACE :
E=D (=90o)
CE=BD (gt)
A:chung
suy ra tam giác ABD =ACE(ch_gn)
suy ra góc B=C(t/ư)
xét tam giác EIB&DIC:
E=D(=90o)
IE=ID
B=C
suy ra tam giácEIB=DIC
suy ra IB=IC
suy ra tam giác BIC cân tại I, suy ra B=C
suy ra:đpcm