Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:1×2×3×4×5×6×7×8×9×10 bằng mấy? Bài 2:5×5×5×5×5×5×5×5×5×5=3628800
Bài 2:9×9×9×9×9×9×9×9×9×9 = 3486784401 (bạn k cho mình nha)


Lời giải:
Ta có: \(\log_3(9^{x+1})\log_3(9^x+1)=3\)
\(\Leftrightarrow (x+1)\log_39\log_3(9^x+1)=3\)
\(\Leftrightarrow (x+1)\log_3(9^x+1)=\frac{3}{2}\)
Từ đây suy ra \(x+1\neq 0\)
\(\Rightarrow \log_3(9^x+1)=\frac{3}{2(x+1)}\)
\(\Leftrightarrow 9^x+1=3^{\frac{3}{2(x+1)}}\) (*)
Đạo hàm vế trái: \((9^x+1)'=\ln 9.9^x>0\), hàm đồng biến
Đạo hàm vế phải: \((3^{\frac{3}{2(x+1)}})'=\frac{-3}{2(x+1)^2}.\ln 3.3^{\frac{3}{2(x+1)}}<0\), hàm nghịch biến
Do đó PT (*) có một nghiệm duy nhất.
Đến đây việc còn lại là dò nghiệm duy nhất đó.
\(x\approx 0,3795\)

*Đâu phải chia lúc nào cũng lớn hơn trừ đâu bạn,
VD: 10 : 5 = 1, Mà 10 - 5 = 5,
Vậy 10 : 5 < 10 - 5 (vì 1 < 5)
*Hay lấy ví dụ của bạn thì 10 : 9 = 1, (1) Mà 10 - 9 = 1
Vậy 10 : 9 > 10 - 9
*Cũng có trường hợp bằng nhau, ví dụ như: 4 : 2 = 2 Mà 4 - 2 = 2
Vậy 4 : 2 = 4 - 2
hoctot

Ý bạn là \(f(x)=\frac{1}{9+x^2}+\frac{3}{9+x^2}\) hay thế nào? Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo để được hỗ trợ tốt hơn).

Xét hàm \(f\left(x\right)=\dfrac{1}{9^x-3}+\dfrac{1}{3^x-9}\) có \(f'\left(x\right)=-\dfrac{9^x.ln9}{\left(9^x-3\right)^2}-\dfrac{3^x.ln3}{\left(3^x-9\right)^2}< 0\)
\(\Rightarrow\) Hàm luôn nghịch biến trên miền xác định
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\dfrac{1}{3}-\dfrac{1}{9}=-\dfrac{4}{9}\) ; \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=0\) ; \(f\left(4\right)>0\)
\(\lim\limits_{x\rightarrow0,5^+}f\left(x\right)=+\infty;\lim\limits_{x\rightarrow0,5^-}f\left(x\right)=-\infty;\lim\limits_{x\rightarrow2^-}f\left(x\right)=-\infty;\lim\limits_{x\rightarrow2^+}f\left(x\right)=+\infty\)
BBT:
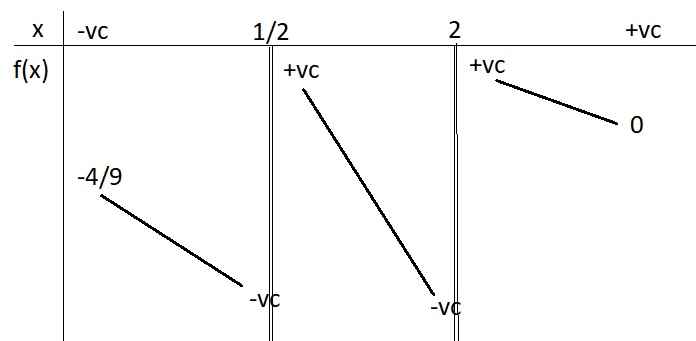
Xét hàm \(g\left(x\right)=x+\left|x-4\right|+a=\left\{{}\begin{matrix}a+4\text{ nếu }x\le4\\2x+a-4\text{ nếu }x\ge4\end{matrix}\right.\)
Từ BBT ta thấy:
- Nếu \(a\ge-3\Rightarrow g\left(x\right)\) cắt f(x) tại 2 điểm phân biệt thỏa mãn \(x< 4\)
- Nếu \(a=-4\Rightarrow g\left(x\right)\) cắt f(x) tại 2 điểm pb thỏa mãn \(x_1< 4< x_2\)
- Nếu \(a\le-5\) \(\Rightarrow g\left(x\right)\) cắt f(x) tại 3 điểm pb thỏa mãn \(x_1< x_2< 4< x_3\) (loại)
Vậy \(a=\left\{-1;-2;-3;-4\right\}\)

Đặt \(\sqrt[3]{2}=a\Leftrightarrow a^3=2\). Ta chứng minh \(\sqrt[3]{a-1}=\frac{a^2-a+1}{\sqrt[3]{9}}\)
Lập phương hai vế ta có :
\(a-1=\frac{\left(a^2-a+1\right)^3}{9}\Leftrightarrow9\left(a-1\right)\left(a+1\right)^3=\left(a+1\right)^3\left(a^2-a+1\right)^3\)
\(\Leftrightarrow9\left(a-1\right)\left(a^3+3a^2+3a+1\right)=\left(a^3+1\right)^3\)
\(\Leftrightarrow9\left(a-1\right)\left(3+3a^2+3a\right)=27\)
\(\Leftrightarrow3\left(a-1\right)\left(a^2+a+1\right)=3\)
\(\Leftrightarrow a^3-1=1\)
\(\Leftrightarrow a^3=2\)
Đẳng thức cuối đúng nên ta có điều phải chứng minh

dấu viết còn sai bảo ai tính