Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
a: Xét ΔOAB có OA=OB=AB
nên ΔOAB đều
=>\(\widehat{AOB}=60^0\)
=>Số đo cung nhỏ AB là 600
Số đo cung lớn AB là 360-60=3000
b: ΔOAB đều
mà OI là đường trung tuyến
nên \(OI=AB\cdot\dfrac{\sqrt{3}}{2}=\dfrac{R\sqrt{3}}{2}\)
c: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
=>M nằm trên đường trung trực của AB(1)
ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI là đường trung trực của AB(2)
Từ (1),(2) suy ra O,I,M thẳng hàng

a) Trong tứ giác AOBM có 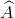 =
= 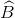 =
= 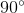 .
.
Suy ra cung AMB +  =
= 
=> cung AMB=  -
- 
=  -
- 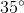
= 
b) Từ 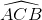 =
=  . Suy ra số đo cung nhỏ AB =
. Suy ra số đo cung nhỏ AB =  và số đo cung lớn AB :
và số đo cung lớn AB :
Cung AB = 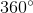 -
-  =
= 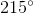

a) Điểm C nằm trên cung nhỏ AB ( hình a)
Số đo cung nhỏ BC = 100º – 45º = 55º
Số đo cung lớn BC = 360º – 55º = 305º
b) Điểm C nằm trên cung lớn AB (hình b)
Số đo cung nhỏ BC = 100º + 45º = 145º
Số đo cung lớn BC = 360º – 145º = 215º
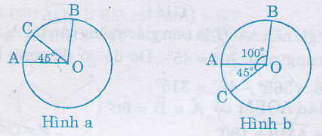
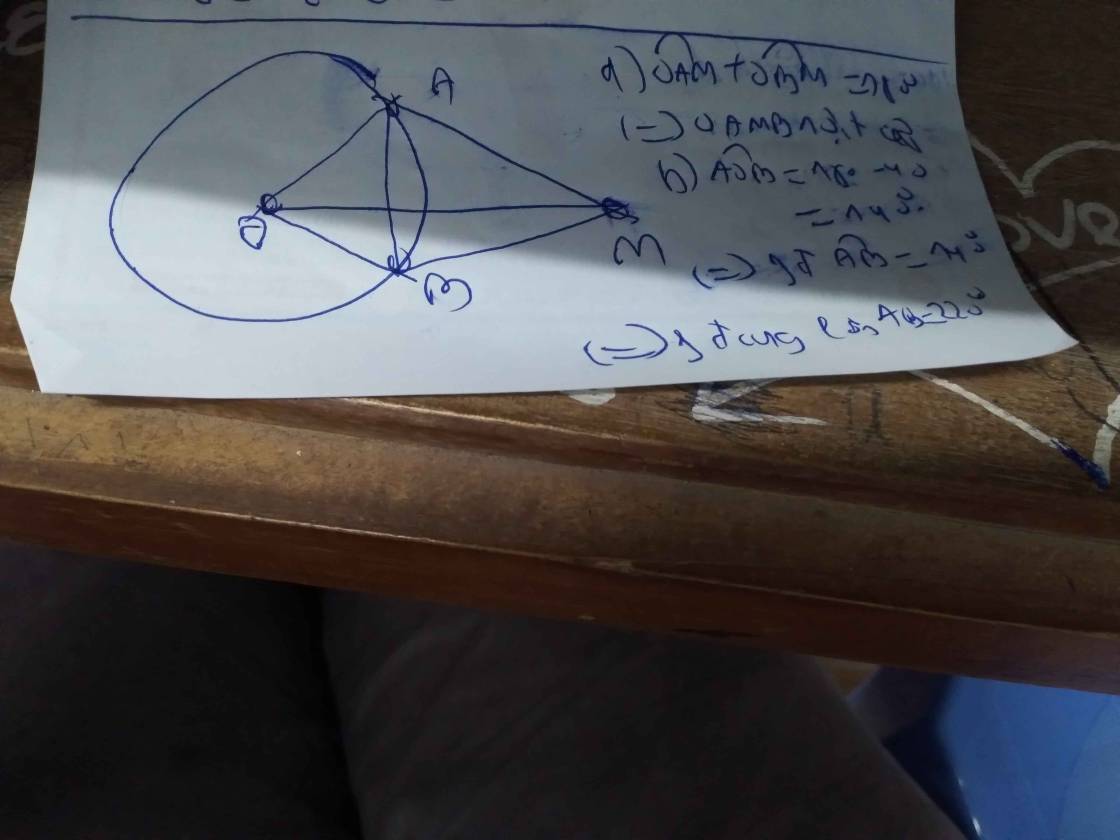
Bài 1.1
a: \(\widehat{AOB}=180^0-35^0=145^0\)
b: Số đo cung nhỏ AB là 120 độ
=>Số đo cung lớn AB là 360-120=240(độ)