
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(|5-x|-17=13\)
\(|5-x|=30\)
\(\Rightarrow\left[{}\begin{matrix}5-x=30\\5-x=-30\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-25\\x=35\end{matrix}\right.\)
Vậy .....
|5-x|-17=13
\(\Rightarrow\left|5-x\right|=13+17\)
\(\Rightarrow\left|5-x\right|=30\)
\(\Rightarrow\left[{}\begin{matrix}5-x=30\\5-x=-30\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5-30\\x=5-\left(-30\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-25\\x=35\end{matrix}\right.\)
vậy x=-25 hoặc x=35
chúc bn học tốt

Các con số 3, 6, 9 gắn liền với cuộc đời của thiên tài Nikola Tesla vì ông cho rằng chúng là chìa khóa giải mã bí mật vũ trụ. ... Tất cả các thiết kế của ông - khoảng 300 trong số đó được cấp bằng sáng chế - đều hướng tới tương lai và đó là lý do mọi người gọi ông là "nhà phát minh ra thế kỷ 20".
đây là mình tham khảo mạng nhé, chứ bn có bổ sung thì bn tự bổ sung nha

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.

HẾT RỒI NHÉ ĐÁP ÁN LÀ :
+ Ta có: y '= 3x2 + 6x + m
+ Để hàm số đã cho đồng biến trên R thì y' ≥ 0,∀x ∈R
+ Yêu cầu bài toán trở thành tìm điều kiện của m để y' ≥ 0,∀x ∈R
Ta có y' = 3x2 + 6x + m, ta có: a = 3>0,Δ = 36 - 12m
Để y' ≥ 0,∀x ∈ R khi Δ ≤ 0 ⇔ 36 - 12m ≤ 0 ⇔ m ≥ 3
Vậy giá trị của tham số m cần tìm là m ≥ 3

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
#Yunk
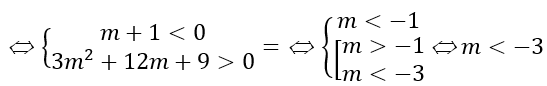
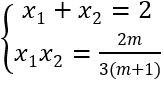
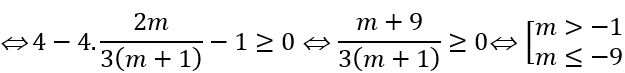
9,12 x 10 ^ 14
bằng 912000000000000