Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn \(\stackrel\frown{AC}\)
\(\widehat{CAM}\) là góc tạo bởi dây cung CA và tiếp tuyến AM
Do đó: \(\widehat{ADC}=\widehat{CAM}\)(Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
hay \(\widehat{MDA}=\widehat{MAC}\)
Xét ΔMDA và ΔMAC có
\(\widehat{MDA}=\widehat{MAC}\)(cmt)
\(\widehat{AMD}\) là góc chung
Do đó: ΔMDA∼ΔMAC(g-g)
⇔\(\dfrac{MD}{MA}=\dfrac{MA}{MC}\)(Các cặp cạnh tương ứng tỉ lệ)
⇔\(MA^2=MC\cdot MD\)(đpcm)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOAM vuông tại A có AH là đường cao ứng với cạnh huyền OM, ta được:
\(MA^2=MH\cdot MO\)(2)
Từ (1) và (2) suy ra \(MH\cdot MO=MC\cdot MD\)(đpcm)
c) để chứng minh EC là tiếp tuyến:
chứng minh tứ giác OECH nội tiếp thì ta sẽ có góc OHE=OCE=90o(đpcm)
=> cần chứng minh tứ giác OECH nội tiếp:
ta có: DOC=DHC (ccc CD)
xét MHC=MDO (tam giác MCH~MOD)= OCD (vì DO=OC)=OHD (cùng chắn OD) => HA là phân giác CHD
DOC=DHC => 1/2 DOC= 1/2 DHC =COE=CHE
mà COE với CHE cùng chắn cung CE trong tứ giác OHCE nên tứ giác đấy nội tiếp => xong :))))

Xét (O) có:
CDA và ABC là 2 góc nội tiếp cùng chắn cung AC
=> góc CDA = góc ABC hay góc MDA= gócMBC
Xét tam giác MDA và tam giác MBC có:
góc MDA = góc MBC(cmt)
góc M chung
=> 2 tam giác trên đồng dạng(g.g)
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>MA.MB=MC.MD

Lời giải:
a)
Xét tam giác MCAMCA và MBCMBC có:
MˆM^ chung
MCAˆ=MBCˆMCA^=MBC^ (góc tạo bởi dây cung và tiếp tuyền thì bằng góc nội tiếp chắn cung đó, cụ thể ở đây là cung ACAC)
⇒△MCA∼△MBC(g.g)⇒△MCA∼△MBC(g.g)
⇒MCMB=MAMC⇒MC2=MA.MB⇒MCMB=MAMC⇒MC2=MA.MB (đpcm)
b)
Theo tính chất tiếp tuyến cắt nhau MC=MDMC=MD
Hơn nữa OC=OD=ROC=OD=R
Do đó MOMO là đường trung trực của CDCD
⇒MO⊥CD⇒MO⊥CD tại HH
⇒MHCˆ=900⇒MHC^=900
Vì MCMC là tiếp tuyến (O)(O) nên MC⊥OC⇒MCOˆ=900MC⊥OC⇒MCO^=900
Xét tam giác MCOMCO và MHCMHC có:
MˆM^ chung
MCOˆ=MHCˆ(=900)MCO^=MHC^(=900)
⇒△MCO∼△MHC(g.g)⇒MCMH=MOMC⇒MC2=MH.MO⇒△MCO∼△MHC(g.g)⇒MCMH=MOMC⇒MC2=MH.MO
Kết hợp với kết quả phần a suy ra MH.MO=MA.MBMH.MO=MA.MB
⇒AHOB⇒AHOB là tứ giác nội tiếp.

a) tứ giác AOBM nội tiếp thì có tâm đường tròn là trung điểm OM
cần CM tứ giác OIMB nội tiếp: dùng tổng hai góc đối cộng với nhau bằng 180o, mà đã có OBM=90o, mà I là trung điểm dây cung CD nên OI vuông góc CD luôn => OIM=90o
Vậy tứ giác OIMB nội tiếp thì tâm đường tròn cũng tại trung điểm OM luôn
b) 5 điểm A,I,O,B,M cùng thuộc 1 đtron
=> tứ giác AIOB nội tiếp => góc AIB=AOB (cùng chắn cung)
tứ giác AIOM nội tiếp => góc AIM=AOM (ccc)
mà góc AOM=1/2AOB=AIM=1/2AIB
=> BIM=1/2AIB (đpcm

vì AM là tiếp tuyến của ( O) => OA⊥AM =>ΔOAM vuông ở A
=> điểm A thuộc đường tròn đường kính OM
vì BM là tiếp tuyến của (O) => OB⊥BM =>ΔOBM vuông ở B
=> điểm B thuộc đường tròn đường kính OM
Vì OH⊥MI=>ΔOHM vuông tại H
=> điểm H thuộc đường tròn đường kính OM
=> 4 điểm O,A,M,B,H cùng thuộc đường tròn đường kính OM

a) Tứ giác MAOB có: \(\widehat{OAM}=90^0\left(0A\perp AM\right);\widehat{OBM}=90^0\left(CB\perp BM\right)\)
=> \(\widehat{OAM}+\widehat{OBM}=180^O\)
=> AOBM nội tiếp (tổng 2 góc đối = 180)
Vì I là tâm=> I là trung điểm OM
b) Tính \(MA^2=3R^2\Rightarrow MC.MD=3R^2\)
c) CM: OM là trung trực AB
=> FA=FB
=> tam giác FAB cân tại F
Gọi H là giao điểm AB và OM
Ta có: OA=OB=AI=R => tam giác OAI đều
=> OAI =60O=> FAB=60o (cùng phụ AFI)
Vậy tam giác AFB đều
d) Kẻ EK vuông góc với FB tại K. Ta có:
\(S_{B\text{EF}}=\frac{1}{2}.FB.EK\)
Mà \(EK\le BE\)( TAM giác BEK vuông tại K)
Lại có: \(BE\le OA\)(LIÊN hệ đường kính và dây cung)
=> \(S_{B\text{EF}}\le\frac{1}{2}.R\sqrt{3}.2R=R^2\sqrt{3}\)
GTLN của \(S_{B\text{EF}}=R^2\sqrt{3}\). kHI ĐÓ BE là đường kính (I)
Kẻ đường kính BG của (I). Vì B và (I) cố định nên BG cố
định . Khi đó vị trí cắt tuyến MCD để \(S_{B\text{EF}}\)đạt GTLN là C là giao điểm của FG với đường tron (O)

a)
MA và MB là các tiếp tuyến của (O)
=> OM _I_ AB mà C thuộc OM
=> AC = BC
OB = OA = OC = OD ( = R)
=> \(\Delta ACD\) vuông tại A và \(\Delta BCD\) vuông tại B
\(\Rightarrow\Delta ACD=\Delta BCD\left(ch-cgv\right)\)
\(\Rightarrow\Delta ACD~\Delta BCD\)
\(\Rightarrow\frac{AC}{BC}=\frac{AD}{BD}\)
\(\Rightarrow AC\times BD=AD\times BC\left(\text{đ}pcm\right)\)
b)
AI là đpg của \(\Delta ACD\)
\(\Rightarrow\frac{IC}{ID}=\frac{AC}{AD}\) mà \(\frac{AC}{AD}=\frac{BC}{BD}\)
\(\Rightarrow\frac{IC}{ID}=\frac{BC}{BD}\)
=> BI là đpg của \(\Delta BCD\) (đpcm)
a) MA và MB là các tiếp tuyến của (O)
=> OM _I_ AB mà C thuộc OM
=> AC = BC
OB = OA = OC = OD ( = R)
=> \Delta ACDΔACD vuông tại A và \Delta BCDΔBCD vuông tại B
\Rightarrow\Delta ACD=\Delta BCD\left(ch-cgv\right)⇒ΔACD=ΔBCD(ch−cgv)
\Rightarrow\Delta ACD~\Delta BCD⇒ΔACD ΔBCD
\Rightarrow\frac{AC}{BC}=\frac{AD}{BD}⇒BCAC=BDAD
\Rightarrow AC\times BD=AD\times BC\left(\text{đ}pcm\right)⇒AC×BD=AD×BC(đpcm)
b)
AI là đpg của \Delta ACDΔACD
\Rightarrow\frac{IC}{ID}=\frac{AC}{AD}⇒IDIC=ADAC mà \frac{AC}{AD}=\frac{BC}{BD}ADAC=BDBC
\Rightarrow\frac{IC}{ID}=\frac{BC}{BD}⇒IDIC=BDBC
=> BI là đpg của \Delta BCDΔBCD (đpcm)
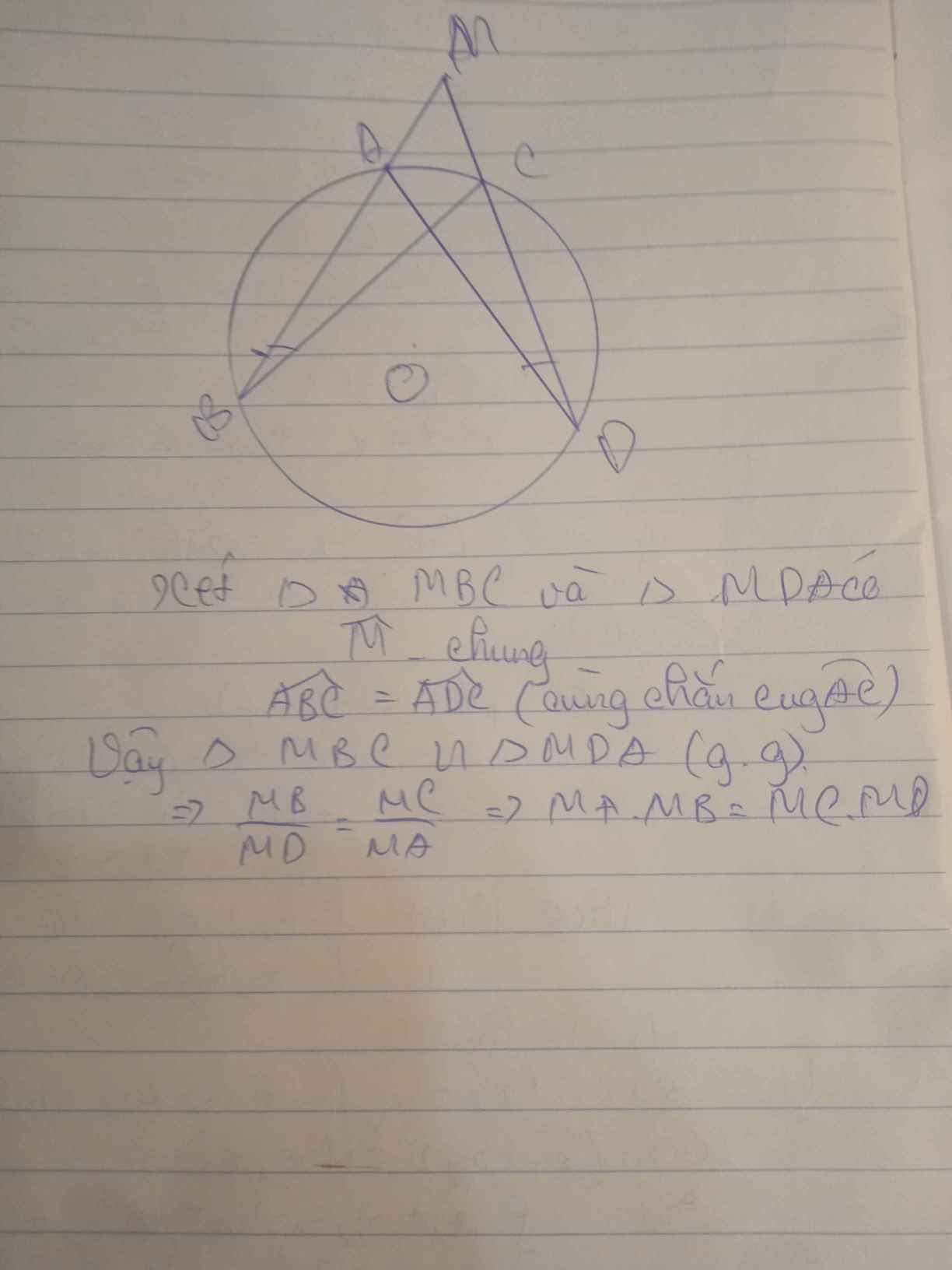
1) Xét (O) có
\(\widehat{ACD}\) là góc nội tiếp chắn \(\stackrel\frown{AD}\)
\(\widehat{MDA}\) là góc tạo bởi tia tiếp tuyến MD và dây cung AD
Do đó: \(\widehat{ACD}=\widehat{MDA}\)(Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
hay \(\widehat{MCD}=\widehat{MDA}\)
Xét ΔMCD và ΔMDA có
\(\widehat{MCD}=\widehat{MDA}\)(cmt)
\(\widehat{CMD}\) chung
Do đó: ΔMCD∼ΔMDA(g-g)
⇒\(\dfrac{MC}{MD}=\dfrac{MD}{MA}\)(Các cặp cạnh tương ứng tỉ lệ)
nên \(MD^2=MC\cdot MA\)(đpcm)