Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
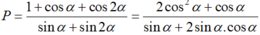
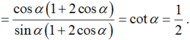

\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)
\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)
\(\Rightarrow P=4\)
\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)
\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)
\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)

\(\dfrac{2sina+cosa}{2sin^3a-cos^3a}=\dfrac{\dfrac{2sina}{cos^3a}+\dfrac{cosa}{cos^3a}}{\dfrac{2sin^3a}{cos^3a}-\dfrac{cos^3a}{cos^3a}}=\dfrac{2tana.\dfrac{1}{cos^2a}+\dfrac{1}{cos^2a}}{2tan^3a-1}\)
\(=\dfrac{2tana\left(1+tan^2a\right)+1+tan^2a}{2tan^3a-1}=...\) (thay số và bấm máy)
Em vẫn ch hiểu tại sao cosa/cos3a lại ra 1/cos2a thầy giải thích giúp em vs ạ

\(P=sin^22x-\left[2sin\dfrac{x}{2}cos\dfrac{x}{2}\left(cos^4\dfrac{x}{2}-sin^4\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx\left(cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}\right)\left(cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx.cosx.1\right]^2\)
\(=sin^22x-\left[\dfrac{1}{2}sin2x\right]^2\)
\(=\dfrac{3}{4}sin^22x=\dfrac{3}{4}\left(1-cos^22x\right)=\dfrac{3}{4}\left(1-\dfrac{1}{4}\right)=\dfrac{9}{16}\)

a/\(sina-1=2sin\dfrac{a}{2}.cos\dfrac{a}{2}-sin^2\dfrac{a}{2}-cos^2\dfrac{a}{2}=-\left(sin\dfrac{a}{2}-cos\dfrac{a}{2}\right)^2\)
b/\(P=\dfrac{cosa+cos5a+2cos3a}{sina+sin5a+2sin3a}=\dfrac{2cos3a.cos2a+2cos3a}{2sin3a.cos2a+2sin3a}=\dfrac{2cos3a\left(cos2a+1\right)}{2sin3a\left(cos2a+1\right)}=cot3a\)
c/\(P=sin\left(30+60\right)=sin90=1\)
d/
\(A=cos\dfrac{2\pi}{7}+cos\dfrac{6\pi}{7}+cos\dfrac{4\pi}{7}\Rightarrow A.sin\dfrac{\pi}{7}=sin\dfrac{\pi}{7}.cos\dfrac{2\pi}{7}+sin\dfrac{\pi}{7}cos\dfrac{4\pi}{7}+sin\dfrac{\pi}{7}.cos\dfrac{6\pi}{7}\)
\(=\dfrac{1}{2}sin\dfrac{3\pi}{7}-\dfrac{1}{2}sin\dfrac{\pi}{7}+\dfrac{1}{2}sin\dfrac{5\pi}{7}-\dfrac{1}{2}sin\dfrac{3\pi}{7}+\dfrac{1}{2}sin\dfrac{7\pi}{7}-\dfrac{1}{2}sin\dfrac{5\pi}{7}\)
\(=-\dfrac{1}{2}sin\dfrac{\pi}{7}\Rightarrow A=-\dfrac{1}{2}\)
e/
\(tan\dfrac{\pi}{24}+tan\dfrac{7\pi}{24}=\dfrac{sin\dfrac{\pi}{24}}{cos\dfrac{\pi}{24}}+\dfrac{sin\dfrac{7\pi}{24}}{cos\dfrac{7\pi}{24}}=\dfrac{sin\dfrac{\pi}{24}cos\dfrac{7\pi}{24}+sin\dfrac{7\pi}{24}cos\dfrac{\pi}{24}}{cos\dfrac{\pi}{24}.cos\dfrac{7\pi}{24}}\)
\(=\dfrac{sin\left(\dfrac{\pi}{24}+\dfrac{7\pi}{24}\right)}{\dfrac{1}{2}cos\dfrac{\pi}{4}+\dfrac{1}{2}cos\dfrac{\pi}{3}}=\dfrac{2sin\dfrac{\pi}{3}}{cos\dfrac{\pi}{4}+cos\dfrac{\pi}{3}}=\dfrac{\sqrt{3}}{\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}+1}\)

Chia tử và mẫu cho cosa ta có:
B=\(\dfrac{4\tan a+5}{2\tan a-3}\). Vì \(\cot a=\dfrac{1}{2}\) nên \(\tan a=2\)
=> B=13
chia tử và mẫu của B cho sina khác 0\(B=\dfrac{4\dfrac{sina}{sina}+5\dfrac{cosa}{sina}}{2\dfrac{sina}{sina}-3\dfrac{cosa}{sina}}=\dfrac{4+5cota}{2-3cota}=\dfrac{4+5\dfrac{1}{2}}{2-3\dfrac{1}{2}}=13\)
vay B = 13
1.
\(cos70+cos50=2cos\dfrac{70+50}{2}.cos\dfrac{70-50}{2}=2.cos60.cos10=2.\dfrac{1}{2}cos10\)
\(cos70+cos50-cos10=0\)
2.\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}=1\Rightarrow tana+tanb+tana.tanb+1=2\Leftrightarrow\left(1+tana\right)\left(1+tanb\right)=2\)