Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Diện tích da phủ kín quả bóng là:
$\4\pi r^2=\pi d^2=24^2\pi = 576\pi$ (cm2)
Diện tích da dùng để khâu bóng:
$576\pi (1+0,02)=587,52\pi$ (cm2)

Từ công thức \(S_{cầu}=4\pi r^2=1256\left(cm^2\right)\)
\(\Rightarrow r^2=\dfrac{1256}{4\pi}\approx100\left(cm\right)\Rightarrow r\approx10\left(cm\right)\)

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3

Câu hỏi của Huy đức - Toán lớp 9 - Học toán với OnlineMath

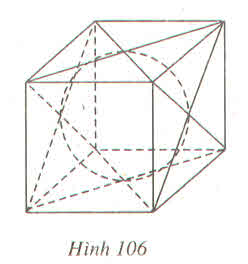
Ta thấy ngay cạnh của hình lập phương gấp đôi bán kính hình cầu
a) Tỉ số cần tính \(\dfrac{6}{\pi}\)
b) Diện tích toàn phần của hình lập phương là \(42cm^2\)
c) Thể tích cần tính xấp xỉ \(244cm^3\)

trả lời
bài này e chưa học đến
nhưng
c có thể vào học 24 hỏi nha
chúc c học tốt
Gọi x là số múi da màu đen , y là số múi da màu trắng \((x,y\inℕ^∗)\)
Bán kính trái bóng : R = 22,3 : 2 = 11,15cm
Diện tích bề mặt trái bóng S= \(4^{\pi}\cdot R^2=1562,3cm^2\)
Ta có hpt : \(\hept{\begin{cases}x+y=32\\37\cdot x+55,9\cdot y=1562,3\end{cases}}\Rightarrow\hept{\begin{cases}x=12\\y=20\end{cases}}\)
Vậy trái bóng có 12 múi da màu đen và 20 múi da màu trắng
Áp dụng công thức tính thể tích hình cầu, ta có:
\(V_{cầu}=\dfrac{4}{3}\pi R^3\)
Mà thể tích hình cầu này là 288dm3 nên ta có \(\dfrac{4}{3}\pi R^3=288\Leftrightarrow\pi R^3=216\Leftrightarrow R^3=\dfrac{216}{\pi}\Leftrightarrow R=\sqrt[3]{\dfrac{216}{\pi}}=\dfrac{6}{\sqrt[3]{\pi}}\left(dm\right)\)
Áp dụng công thức tính diện tích mặt cầu, ta có \(S_{mc}=4\pi R^2=4\pi\left(\dfrac{6}{\sqrt[3]{\pi}}\right)^2=4\pi.\dfrac{36}{\sqrt[3]{\pi^2}}=144.\sqrt[3]{\pi}\approx210,9\left(dm^2\right)\)
Vậy diện tích da để làm nên quả bóng đó là khoảng 210,9dm2.