Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F
Ta có AB = BC = CA, AD = BE = CF
nên AB - AD = BC - BE = CA - CF hay BD = CE = AF.
\(\Delta ABC\) đều \(\Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
Xét hai tam giác ADF và BED có:
BD = AF (cmt)
\(\widehat{A}=\widehat{B}\left(cmt\right)\)
BE = AD (gt)
Vậy: \(\Delta ADF=\Delta BED\left(c-g-c\right)\)
\(\Rightarrow\) DF = DE (hai cạnh tương ứng)
Xét hai tam giác EBD và FCE có:
BD = CE (cmt)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
BE = CF (gt)
Vậy: \(\Delta EBD=\Delta FCE\left(c-g-c\right)\)
\(\Rightarrow\) DE = EF (hai cạnh tương ứng)
Do đó DF = DE = EF. Vậy \(\Delta DEF\) là tam giác đều.

Bài 1 :
a)Tam giác ABC cân tại A => AB=AC=7+2=9(cm)
Xết tam giác AHB có góc H=90o
Theo định lí py-ta-go, ta có::
AB2- AH2= BH2
<=> 81-49=BH2 <=> 32=BH2
Xét tam giác BHC có góc H=900
Theo định lí pi-ta-go, ta có:
BH2+HC2 =BC2
(=) 32+22 =BC2
(=)32+4 = BC2 (=) 36 =BC2 =) BC= 6 Bài 2:Do ΔABC đều nên Aˆ=Bˆ=Cˆ=60o và AB=AC=BC
Mà AD=CF=BE⇒BD=AF=EC
Xét ΔADF và ΔBED có:
AD = BE ( gt )
Aˆ=Bˆ=60o
AF = BD ( cmt )
⇒ΔADF=ΔBED(c−g−c)⇒DF=ED ( cạnh t/ứng ) (1)
Xét ΔADF và ΔCFE có:
AD = CF ( gt )
Aˆ=Cˆ=60o
AF = CE ( cmt )
⇒ΔADF=ΔCFE(c−g−c)⇒DF=FE ( cạnh t/ứng ) (2)
Từ (1) và (2) ⇒DF=DE=FE
⇒ΔDEF đều

bài 1)
tổng 2 tỉ số là: 4+5=9
chiều dài là: (72:9).5=40(m)
chiều rộng là: (72:9).4=32(m)
bài 2)
a) trong tam giác ABC ( góc B bằng 90 độ ), có:
Góc A + Góc B + Góc C=180 độ ( tổng ba góc trong tam giác )
=> Góc A = 180 độ - góc B - góc A = 180 độ - 90 độ - 50 độ = 40 độ
b) Xét tam giác ABE và tam giác ADE có:
AB=AD (gt)
góc BAE = góc DAE ( AE là phân giác góc A )
AE là cạnh chung ( gt )
=> tam giác ABE = tam giac ADE ( cgc )
=> góc ABE = góc ADE ( dpcm )

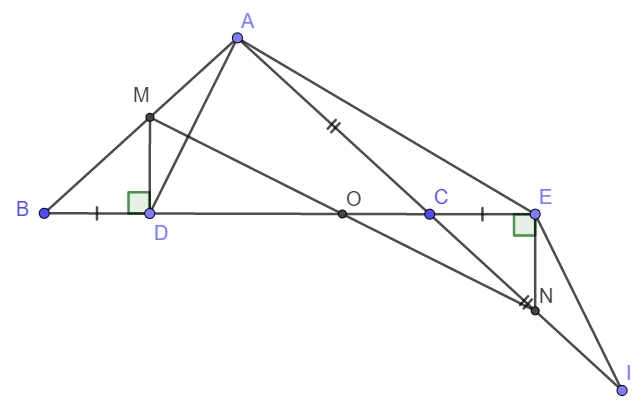
1)
+) Ta thấy \(\widehat{ECI}=\widehat{ACB}\) (Hai góc đối đỉnh)
Mà \(\widehat{ACB}=\widehat{ABC}\) (Tam giác ABC cân tại A)
nên \(\widehat{ECI}=\widehat{DBA}\)
Xét tam giác ABD và tam giác ICE có:
BD = CE (gt)
\(\widehat{DBA}=\widehat{ECI}\left(cmt\right)\)
CI = BA ( Cùng bằng AC)
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right)\)
+) Xét tam giác AEI, theo bất đẳng thức trong tam giác, ta có:
AI > AE + EI
Lại có do \(\Delta ABD=\Delta ICE\Rightarrow AD=IE\)
Vậy nên ta có AI > AE + AD \(\Rightarrow2AC>AD+AE\Rightarrow AB+AC>AD+AE\)
2) Do \(\Delta ABD=\Delta ICE\Rightarrow\widehat{MBD}=\widehat{NCE}\)
Vậy thì ta thấy ngay \(\Delta BDM=\Delta CEN\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BM=CN\)
3) Ta thấy AB + AC = AM + MB + AC = AM + CN + AC = AM + AN
Ta cần chứng minh BC < MN.
Do BD = EC nên AC = DE
Xét tam giác vuông MDO ta có DO < MO (Quan hệ đường vuông góc, đường xiên)
Ta cũng có OE < ON
Vậy nên DE < MN hay BC < MN
Từ đó: AB + AC + BC < AM + AN + MN
Hay \(P_{AMN}>P_{ABC}\)

do tam giác abc cân tại a
=>góc abc=180-2*góc a
do am=an
=>tam giác amn can taị a
=>góc amn=180-2*góc a
=>góc amn=góc abc(vì cùng bằng
180-2*góc a)
mà hai góc này ở vị trí so le trong
=>mn song song vs ab
xét 2 tam giác abn và acm có
chung góc a
am=an
ab=ac
=>tg abn=tg acm
=>bm=cm(2 cạnh tương ứng)
cau 2
theo đề bài ta có
tg abc đều =>ab=bc=ca
ad=be=cf
=>ab-ad=bc-be=ac-cf
hay bd=ce=af
xét 3 tg ade,bed và cef ta có
góc a=gócb=gócc
ad=be=cf
bd=ce=af
=> tg ade= tg bed= tg cef
=>de=df=ef
=>tg def là tg đều

Tự vẽ hình nha !
Xét tam giác đều ABC có :
\(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
Xét tam giác đều MDC có :
\(\widehat{DMC}=\widehat{MCD}=\widehat{CDM}=60^0\)
Ta có :
Góc ACB = ACM + MCB = 600
Góc MCD = MCB + BCD = 600
=> Góc ACM = Góc BCD
Xét tam giác ACM và tam giác BCD có :
AC = BC
CD = CM => tam giác ACM = tam giác BCD
Góc ACM = Góc BCD
Bài 1 :
A B C D 12inch 20inch
Ta có : \(1inch=2,54cm\)
Nên : \(\left\{{}\begin{matrix}BC=12.2,54=30,48\left(cm\right)\\AC=20.2,54=50,8\left(cm\right)\end{matrix}\right.\)
Theo hình vẽ ta có :
Xét \(\Delta ABC\) có :
\(\widehat{B}=90^o\) (tính chất hình chữ nhật - gt)
=> \(\Delta ABC\) vuông tại B
Có : \(AB^2=AC^2-BC^2\) (Theo định lí PITAGO)
=> \(AB^2=\left(50,8\right)^2-\left(30,48\right)^2=1652\)
\(\Rightarrow AB=\sqrt{1652}\approx41\left(cm\right)\)
Vậy chiều dài của máy thu hình khoảng 41cm