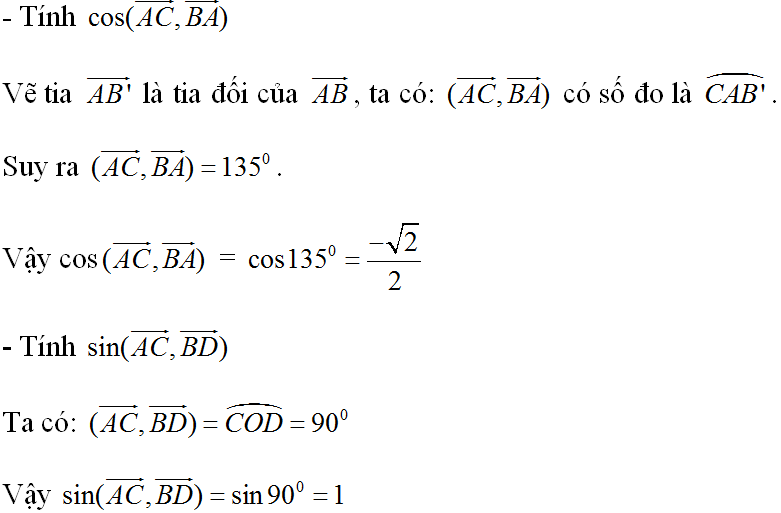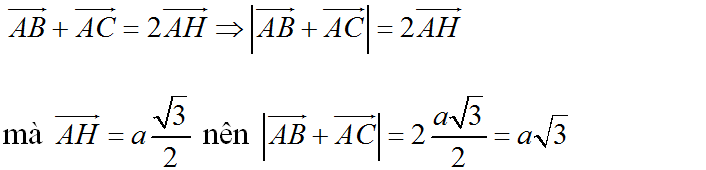Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tam giác ABC vuông tại A và \(\widehat{B}=30^o\) \(\Rightarrow C=60^o\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=150^o;\)\(\left(\overrightarrow{BA},\overrightarrow{BC}\right)=30^o;\left(\overrightarrow{AC},\overrightarrow{CB}\right)=120^o\)
\(\left(\overrightarrow{AB},\overrightarrow{AC}\right)=90^o;\left(\overrightarrow{BC},\overrightarrow{BA}\right)=30^o\).Do vậy:
a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)
\(=\cos150^o+\sin30^o+\tan60^o\)
\(=-\frac{\sqrt{3}}{2}+\frac{1}{2}+\sqrt{3}\)
\(=\frac{\sqrt{3}+1}{2}\)
b) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{AB}\right)+\cos\left(\overrightarrow{CA},\overrightarrow{BA}\right)\)
\(=\sin90^o+\cos30^o+\cos0^o\)
\(=1+\frac{\sqrt{3}}{2}\)
\(=\frac{2+\sqrt{3}}{2}\)

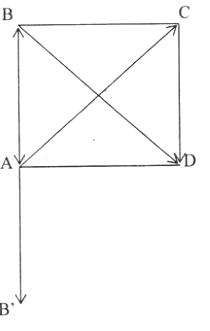
A B C D B' O
\(cos\left(\overrightarrow{AC};\overrightarrow{BA}\right)=cos\left(\overrightarrow{AC};\overrightarrow{AB'}\right)=cos\widehat{CAB'}=cos135^o\)\(=\dfrac{\sqrt{2}}{2}\).
\(sin\left(\overrightarrow{AC};\overrightarrow{BD}\right)=sin90^o=1\) do \(AC\perp BD\).
\(cos\left(\overrightarrow{AB};\overrightarrow{CD}\right)=cos180^o=-1\) do hai véc tơ \(\overrightarrow{AB};\overrightarrow{CD}\) ngược hướng.

Lời giải:
\(|\overrightarrow{AB}|=BC\cos B=2.\cos 60^0=1\) (cm)
\(|\overrightarrow{AC}|=BC\sin B=2.\sin 60^0=\sqrt{3}\) (cm)
------------------
Do tam giác $ABC$ vuông tại $A$ nên $\overrightarrow{AB}\perp \overrightarrow{AC}\Rightarrow \overrightarrow{AB}.\overrightarrow{AC}=0$. Do đó:
\(|\overrightarrow{AB}+\overrightarrow{AC}|^2=(\overrightarrow{AB}+\overrightarrow{AC})^2=AB^2+AC^2+2\overrightarrow{AB}.\overrightarrow{AC}\)
\(=BC^2+0=BC^2=4\) (cm)
$\Rightarrow |\overrightarrow{AB}+\overrightarrow{AC}|=2$ (cm)
Tương tự:
\(|\overrightarrow{AB}-\overrightarrow{AC}|^2=AB^2+AC^2-2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2=BC^2=4\)
$\Rightarrow |\overrightarrow{AB}-\overrightarrow{AC}|=2$ (cm)
Lời giải:
\(|\overrightarrow{AB}|=BC\cos B=2.\cos 60^0=1\) (cm)
\(|\overrightarrow{AC}|=BC\sin B=2.\sin 60^0=\sqrt{3}\) (cm)
------------------
Do tam giác $ABC$ vuông tại $A$ nên $\overrightarrow{AB}\perp \overrightarrow{AC}\Rightarrow \overrightarrow{AB}.\overrightarrow{AC}=0$. Do đó:
\(|\overrightarrow{AB}+\overrightarrow{AC}|^2=(\overrightarrow{AB}+\overrightarrow{AC})^2=AB^2+AC^2+2\overrightarrow{AB}.\overrightarrow{AC}\)
\(=BC^2+0=BC^2=4\) (cm)
$\Rightarrow |\overrightarrow{AB}+\overrightarrow{AC}|=2$ (cm)
Tương tự:
\(|\overrightarrow{AB}-\overrightarrow{AC}|^2=AB^2+AC^2-2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2=BC^2=4\)
$\Rightarrow |\overrightarrow{AB}-\overrightarrow{AC}|=2$ (cm)

Gọi M là trung điểm của BC
Xét ΔABC có AM là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)
\(\Leftrightarrow\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=a\)

\(AB\perp AC\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
Đặt \(x=\left|\overrightarrow{AB}-\overrightarrow{AC}\right|\Rightarrow x^2=AB^2+AC^2-2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2=a^2+b^2\)
\(\Rightarrow x=\sqrt{a^2+b^2}\)
\(y=\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\Rightarrow y^2=AB^2+AC^2+2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2=a^2+b^2\)
\(\Rightarrow y=\sqrt{a^2+b^2}\)