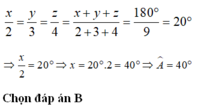Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng số đo các góc của hình tam giác luôn bằng 360 độ
Số đo của góc A là:360:(3+5+7)x3=72 độ
Số đo của góc B là:72:3x5=120 độ
Số đo của góc C là:360-120-72=168 độ

Lời giải:
Tam giác $ABC$ vuông tại $C$ nên $\widehat{C}=90^0$.
$\widehat{A}+\widehat{B}=180^0-\widehat{C}=180^0-90^0=90^0$
Vì $\widehat{A}, \widehat{B}$ tỉ lệ nghịch với $\frac{1}{2}, \frac{2}{5}$ nên:
$\widehat{A}.\frac{1}{2}=\widehat{B}.\frac{2}{5}$
$\Rightarrow \widehat{A}=\widehat{B}.\frac{2}{5}:\frac{1}{2}=\widehat{B}.\frac{4}{5}$
$\Rightarrow \widehat{A}+\widehat{B}=\frac{9}{5}\widehat{B}$
$\Rightarrow 90^0=\frac{9}{5}\widehat{B}$
$\Rightarrow \widehat{B}=50^0$
$\widehat{A}=90^0-\widehat{B}=90^0-50^0=40^0$

c) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=180^0-40^0=140^0\)
Ta có: \(\widehat{B}:\widehat{C}=3:4\)(gt)
nên \(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}\)
mà \(\widehat{B}+\widehat{C}=140^0\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{B}+\widehat{C}}{3+4}=\dfrac{140^0}{7}=20^0\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{\widehat{B}}{3}=20^0\\\dfrac{\widehat{C}}{4}=20^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=60^0\\\widehat{C}=80^0\end{matrix}\right.\)
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\left(40^0< 60^0< 80^0\right)\)
mà cạnh đối diện với \(\widehat{A}\) là cạnh BC
cạnh đối diện với \(\widehat{B}\) là cạnh AC
và cạnh đối diện với \(\widehat{C}\) là cạnh AB
nên BC<AC<AB