Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Với \(x\in\left[0;1\right]\) => x - 2 < 0 => |x - 2| = - (x -2)
Khi đó, \(f\left(x\right)=2\left(m-1\right)x+\frac{m\left(x-2\right)}{-\left(x-2\right)}=2\left(m-1\right)x-m\)
Để f(x) < 0 với mọi \(x\in\left[0;1\right]\) <=> \(2\left(m-1\right)x-m<0\) (*) với mọi \(x\in\left[0;1\right]\)
+) Xét m - 1 > 0 <=> m > 1
(*) <=> \(x<\frac{m}{2\left(m-1\right)}\). Để (*) đúng với mọi \(x\in\left[0;1\right]\) <=> \(\frac{m}{2\left(m-1\right)}\ge1\) <=> 2(m -1) \(\le\)m <=> m \(\le\) 2 <=> m \(\le\) 2
Kết hợp điều kiện m > 1 =>1 < m \(\le\) 2
+) Xét m = 1 thì (*) <=> -1 < 0 luôn đúng => m =1 thỏa mãn
+) Xét m - 1 < 0 <=> m < 1
(*) <=> \(x>\frac{m}{2\left(m-1\right)}\). Để (*) đúng với mọi \(x\in\left[0;1\right]\) <=> \(\frac{m}{2\left(m-1\right)}\le0\) <=> m \(\ge\) 0 (do m< 1 ). Kết hợp m < 1 => 0 \(\le\) m < 1
Kết hợp các trường hợp : Với 0 \(\le\)m \(\le\) 2 thì .....
b) Hoành độ giao điểm của đò thị hàm số với Ox là nghiệm của Phương trình : \(2\left(m-1\right)x+\frac{m\left(x-2\right)}{\left|x-2\right|}=0\) (1)
Đồ thị hàm số cắt Ox tại điểm có hoành độ xo thuộc (1;2) => xo < 2 => |xo - 2| = - (xo - 2)
xo là nghiệm của (1) <=> \(2\left(m-1\right)x_o+\frac{m\left(x_o-2\right)}{\left|x_o-2\right|}=0\) <=> \(2\left(m-1\right)x_o-m=0\)
+) Xét m \(\ne\) 1 thì (2)<=> \(x_o=\frac{m}{2\left(m-1\right)}\). Vì 1 < xo < 2 nên \(1<\frac{m}{2\left(m-1\right)}<2\) <=> \(\begin{cases}\frac{m}{2\left(m-1\right)}-1>0\\\frac{m}{2\left(m-1\right)}-2<0\end{cases}\) <=> \(\begin{cases}\frac{-m+2}{2\left(m-1\right)}>0\left(a\right)\\\frac{-3m+4}{2\left(m-1\right)}<0\left(b\right)\end{cases}\)
Giải (a) <=> 1 < m < 2
Giải (b) <=> m < 1 hoặc m > 4/3
Kết hợp nghiệm của (a) và (b) => 4/3 < m < 2
+) Xét m = 1 thì (2) <=> -1 = 0 Vô lí
Vậy Với 4/3 < m < 2 thì đồ thị hàm số cắt Ox tại điểm thuộc (1;2)

Khi m = 2 : y = x + 5
TXĐ : D = R.
Tính biến thiên :
- a = 1 > 0 hàm số đồng biến trên R.
bảng biến thiên :
x | -∞ | +∞ | |
y | -∞ | +∞ |
Bảng giá trị :
x | 0 | -5 |
y | 5 | 0 |
Đồ thị hàm số y = x + 5 là đường thẳng đi qua hai điểm A(0, 5) và B(-5; 0).
b/(dm) đi qua điểm A(4, -1) :
4 = (m -1)(-1) +2m +1
<=> m = 2
3. hàm số nghịch biến khi : a = m – 1 < 0 <=> m < 1
4.(dm) đi qua điểm cố định M(x0, y0) :
Ta được : y0 = (m -1)( x0) +2m +1 luôn đúng mọi m.
<=> (x0 + 2) m = y0 – 1 + x0(*)
(*) luôn đúng mọi m khi :
x0 + 2= 0 và y0 – 1 + x0 = 0
<=> x0 =- 2 và y0 = 3
Vậy : điểm cố định M(-2, 3)

Phương trình hoành độ giao điểm là:
\(x^2+\left(2m-3\right)x+5-4m=2mx-4m+3\)
=>\(x^2+\left(2m-3\right)x+5-4m-2mx+4m-3=0\)
=>\(x^2+x\left(2m-3-2m\right)+5-4m+4m-3=0\)
=>\(x^2-3x+2=0\)
=>\(\left(x-1\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Khi x=1 thì \(y=2m\cdot1-4m+3=2m-4m+3=-2m+3\)
Khi x=2 thì \(y=2m\cdot2-4m+3=3\)
Vậy: (dm) và (P) luôn cắt nhau tại điểm A(2;3) cố định

a) Điểm A(x0;y0) thuộc đồ thị (G) của hàm số y = f(x) có tập xác định D khi và chỉ khi: 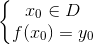
Tập xác định của hàm số y = 3x2 – 2x + 1 là D = R.
Ta có : -1 ∈ R, f(- 1) = 3(- 1)2 – 2(- 1) + 1 = 6
Vậy điểm M(- 1;6) thuộc đồ thị hàm số đã cho.
b) Ta có: 1 ∈ R, f(1) = 3 (1)2 – 2(1) + 1 = 2 ≠ 1.
Vậy N(1;1) không thuộc đồ thị đã cho.
c) P(0;1) thuộc đồ thị đã cho.
