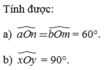Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Vì OA nằm trong MON
=> Tia OA nằm giữa OM,ON
=> MOA+AON=120
=> 90+AON=120
=>AON=30 (1)
Vì OB nằm trong MOB
=>OB NẰM giữa OM,ON
=>MOB+BON=MON
=>MOB+90=120
=>MOB=30 (2)
Từ (1) và(2)=> MOB=AON (dpcm)
b) vì Ox là tia phan giác của AON
=> Ox nằm giữa OA,ON
=>xOA= AON/2=15
VìOy là tia phân giác của BOM
=>yOM=BOM/2=15
=>xOA=yOM
=>xOA+AOB+BOy=xOy
Mà yOM+AOB+BOy=AOM+90
Do AOx=yOM
=>xOy=AOM=90
=> Ox vuông góc với Oy(dpcm)
c)NOx và BOy
xOA và yOM
NOA và BOM
AOB và MON
O N a b M y x
a, Vì \(Oa\perp OM\)
\(\Leftrightarrow aOM=90^0\)
Mà \(MOa+aON=MON\)
\(\Leftrightarrow aON=MON-MOa=120^0-90^0=30^0\)
Vì \(Ob\perp ON\)
\(\Leftrightarrow bOn=90^0\)
Mà \(bOM+bON=MON\)
\(\Leftrightarrow bOM=MON-bOn=120^0-90^0=30^0\)
Vậy \(aON=bOM\)
b, Ta có :
\(aOx=xON=\dfrac{aON}{2}=\dfrac{30^0}{2}=15^0\) (do Ox là tia phân giác của aON)
\(MOy=yOb=\dfrac{mOb}{2}=\dfrac{30^0}{2}=15^0\) (do Oy là tia phân giác của MOy)
Ta có :
\(MON-MOy-xON=yOx\)
\(\Leftrightarrow yOx=120^0-15^0-15^0=90^0\)
Vậy \(Ox\perp Oy\)
a: \(\widehat{AON}+\widehat{AOM}=\widehat{MON}\)
nên \(\widehat{AON}=120^0-90^0=30^0\left(1\right)\)
\(\widehat{BOM}+\widehat{BON}=\widehat{MON}\)
nên \(\widehat{BOM}=120^0-90^0=30^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AON}=\widehat{BOM}\)
b: Sửa đề: Oy là phân giác của góc MOB
\(\widehat{MOy}=\dfrac{30^0}{2}=15^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OM, ta có: \(\widehat{MOy}< \widehat{MON}\)
nên tia Oy nằm giữa hai tia OM và ON
=>\(\widehat{MOy}+\widehat{yON}=\widehat{MON}\)
hay \(\widehat{yON}=105^0\)
\(\widehat{NOx}=\dfrac{30^0}{2}=15^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia ON, ta có: \(\widehat{NOx}< \widehat{NOy}\)
nên tia Ox nằm giữa hai tia OM và Oy
=>\(\widehat{xOM}+\widehat{xOy}=\widehat{MOy}\)
=>\(\widehat{xOy}=90^0\)(đpcm)
,ngày mai tớ đi hok rùi
.huhu
.mấy anh chị CTV hok giỏi thì giúp em vs
Tương tự 5. Tính được:
a) a O n ^ = b O m ^ = 60°. b) x O y ^ = 90°
