Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔBAC nội tiếp
AC là đường kính
Do đó: ΔBAC vuông tại B
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BC}=\dfrac{1}{2}\cdot60^0=30^0\)
Gọi H là giao điểm của BD với AC
BD\(\perp\)AC nên BD\(\perp\)AC tại H
ΔOBD cân tại O
mà OH là đường cao
nên H là trung điểm của BD
Xét ΔCBD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCBD cân tại C
=>CB=CD
Xét ΔCOD và ΔCOB có
CD=CB
OD=OB
CO chung
Do đó: ΔCOD=ΔCOB
=>\(\widehat{COD}=\widehat{COB}\)
=>\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}=60^0\)
Xét ΔBAC vuông tại B có \(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BCA}+30^0=90^0\)
=>\(\widehat{BCA}=60^0\)
Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{BCA}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}\)
=>\(sđ\stackrel\frown{AB}=2\cdot\widehat{BCA}=120^0\)
DF//AC
DB\(\perp\)AC
Do đó: DF\(\perp\)DB
=>ΔDFB vuông tại D
ΔDFB vuông tại D
nên ΔDFB nội tiếp đường tròn đường kính BF
mà ΔDFB nội tiếp (O)
nên O là trung điểm của BF
=>OA//DF
=>\(\widehat{BFD}=\widehat{BOH}=\widehat{BOC}\)(hai góc đồng vị)
=>\(\widehat{BFD}=60^0\)
ΔBDF vuông tại D
=>\(\widehat{BFD}+\widehat{FBD}=90^0\)
=>\(\widehat{FBD}+60^0=90^0\)
=>\(\widehat{FBD}=30^0\)
Xét (O) có
\(\widehat{FBD}\) là góc nội tiếp chắn cung FD
Do đó: \(\widehat{FBD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{FD}\)
=>\(sđ\stackrel\frown{FD}=2\cdot\widehat{FBD}=2\cdot\)30=60 độ

a: góc AOC; góc BOD; góc AOD; góc BOC
b: góc COB=góc AOD=60 độ
=>sđ cung BC=60 đọ
góc AOC=180-60=120 độ
=>sđ cung AC=120 độ
c: sđ cung AC>sđ cung AD
=>AD>AC


Ta chứng minh A D ^ = B E ^ , mà CD ⊥ AB nên từ đó suy ra
* Cách khác:Chứng minh A O C ^ = B O E ^ => ĐPCM

a: Xét (O) có
ΔABC nội tiếp
AC là đường kính
Do đó: ΔABC vuông tại B
ΔBAC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
Xét ΔBAC vuông tại B có
\(sinBAC=\dfrac{BC}{AC}=\dfrac{1}{2}\)
nên \(\widehat{BAC}=30^0\)
b: ΔOAB cân tại O
mà OH là đường cao
nên OH là phân giác của \(\widehat{AOB}\)
Xét ΔOAD và ΔOBD có
OA=OB
\(\widehat{AOD}=\widehat{BOD}\)
OD chung
Do đó: ΔOAD=ΔOBD
=>\(\widehat{OAD}=\widehat{OBD}=90^0\)
=>DB là tiếp tuyến của (O)
c: ΔABC vuông tại B
=>\(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BCA}=90^0-30^0=60^0\)
Xét ΔOBC có OB=OC và \(\widehat{BCO}=60^0\)
nên ΔOBC đều
=>ΔBOC cân tại B
ΔBOC cân tại B
mà BM là đường cao
nên M là trung điểm của OC
ΔOBE cân tại O
mà OM là đường cao
nên M là trung điểm của BE
Xét tứ giác OBCE có
M là trung điểm chung của OC và BE
nên OBCE là hình bình hành
Hình bình hành OBCE có OB=OE
nên OBCE là hình thoi

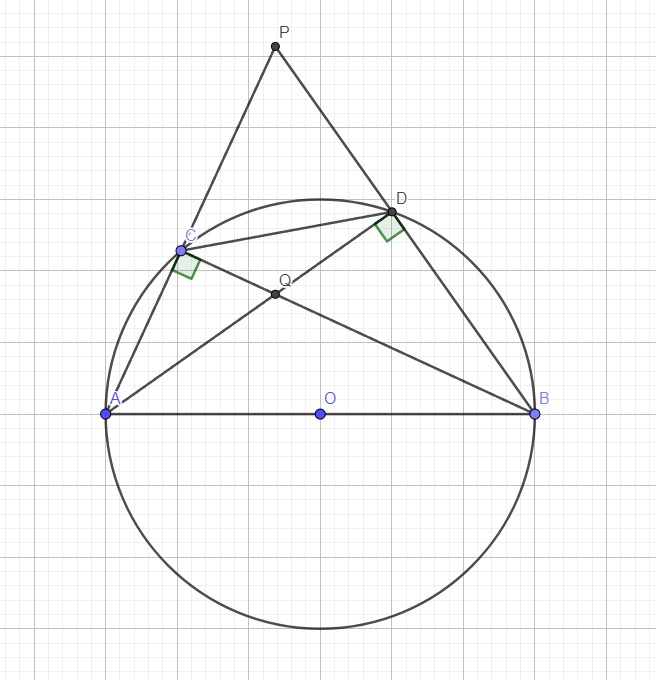
Do \(OC=OD=CD=R\Rightarrow\Delta OCD\) là tam giác đều
\(\Rightarrow\widehat{COD}=60^0\)
Mà \(\widehat{CAD}=\dfrac{1}{2}\widehat{COD}\) (góc nt và góc ở tâm cùng chắn CD)
\(\Rightarrow\widehat{CAD}=30^0\)
AB là đường kính nên \(\widehat{ADB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ADB}=90^0\)
\(\Rightarrow\widehat{ADP}=90^0\Rightarrow\widehat{APB}=180^0-\left(90^0+30^0\right)=60^0\)
Tương tự ta có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\Rightarrow\widehat{BCP}=90^0\)
\(\Rightarrow\widehat{CQD}=360^0-\left(\widehat{APB}+\widehat{ADP}+\widehat{ACB}\right)=360^0-\left(60^0+90^0+90^0\right)=120^0\)
\(\Rightarrow\widehat{AQB}=\widehat{CQD}=120^0\) (2 góc đối đỉnh)