Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: AB//DE(gt)
CD⊥AB(gt)
Do đó: DE⊥CD(Định lí 2 từ vuông góc tới song song)
⇔\(\widehat{CDE}=90^0\)
Xét ΔCDE có \(\widehat{CDE}=90^0\)(cmt)
nên ΔCDE vuông tại D(Định nghĩa tam giác vuông)
⇔D nằm trên đường tròn đường kính CE
⇔C,D,E nằm trên đường tròn đường kính CE
mà C,D,E cùng nằm trên (O)(gt)
nên CE là đường kính của (O)
hay C,O,E thẳng hàng(đpcm)

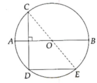
a, Tính được sđ B E ⏜ = 50 0
b, Chứng minh được sđ
C
B
E
⏜
=
180
0
=> C, O, E thẳng hàng (ĐPCM)

a: AM//BN
=>AMBN là hình thang
=>góc MAN+góc ANB=180 độ
=>góc NAM=góc AMB
=>AN//MB
mà AM//BN
nên AMBN là hình bình hành
=>BM=AD và AB cắt MN tại trung điểm của mỗi đường
=>O là trung điểm của MN
b: MD//AB
Xét ΔMDN có
góc MDN là góc nội tiếp chắn nửa đường tròn
=>góc MDN=90 độ
=>MD vuông góc DN
=>DN vuông góc AB
c: ΔODN cân tại O
mà OE là đường cao
nên E là trung điểm của DN
=>DE=EN




Ta chứng minh A D ^ = B E ^ , mà CD ⊥ AB nên từ đó suy ra
* Cách khác:Chứng minh A O C ^ = B O E ^ => ĐPCM