Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

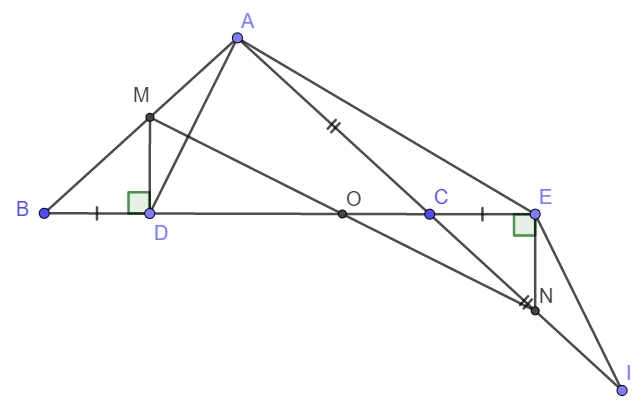
1)
+) Ta thấy \(\widehat{ECI}=\widehat{ACB}\) (Hai góc đối đỉnh)
Mà \(\widehat{ACB}=\widehat{ABC}\) (Tam giác ABC cân tại A)
nên \(\widehat{ECI}=\widehat{DBA}\)
Xét tam giác ABD và tam giác ICE có:
BD = CE (gt)
\(\widehat{DBA}=\widehat{ECI}\left(cmt\right)\)
CI = BA ( Cùng bằng AC)
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right)\)
+) Xét tam giác AEI, theo bất đẳng thức trong tam giác, ta có:
AI > AE + EI
Lại có do \(\Delta ABD=\Delta ICE\Rightarrow AD=IE\)
Vậy nên ta có AI > AE + AD \(\Rightarrow2AC>AD+AE\Rightarrow AB+AC>AD+AE\)
2) Do \(\Delta ABD=\Delta ICE\Rightarrow\widehat{MBD}=\widehat{NCE}\)
Vậy thì ta thấy ngay \(\Delta BDM=\Delta CEN\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BM=CN\)
3) Ta thấy AB + AC = AM + MB + AC = AM + CN + AC = AM + AN
Ta cần chứng minh BC < MN.
Do BD = EC nên AC = DE
Xét tam giác vuông MDO ta có DO < MO (Quan hệ đường vuông góc, đường xiên)
Ta cũng có OE < ON
Vậy nên DE < MN hay BC < MN
Từ đó: AB + AC + BC < AM + AN + MN
Hay \(P_{AMN}>P_{ABC}\)

Kẻ DK vuông góc với BC.
Xét tam giác abd vuông và tam giácadk vuông có
AD:cnhj chung
A1=A2(ad là tia phân giác)
suy ra tam giác abd=tam giác adk
suy ra bD=DK(cạnh tương ứng)1
Có Dc>DK(tam giác dbk vuông)2
từ 1 và 2 suy ra Dc>bD(3)
Có góc E+D2=90 độ(tam giác cde vuông)
A1+D=90 độ(tam giác abd vuông)
A1=A2(cmt)
suy ra A2=E
suy ra tam giác ACE cân tại C
suy ra AC=CE
Ma AC>AB(tam giác abc vuông)
suy ra EC>AB(4)
Từ 3 và 4 suy ra EC^2>AB^2 ; DC^2>BD^2
suy ra EC^2+DC^2>AB^2+BD^2
suy ra ED^2>AD^2
suy ra ED>AD(5)
Từ 3, 4 và 5 suy ra DE+DC+CE>AB+AB+BD
suy ra chu vi tam giác DCE lớn hơn chu vi tam hiacs ABC

A B F C E D 1 2
a) AB // CE \(\Rightarrow\widehat{E}=\widehat{A}_2\)( hai góc so le trong )
mà \(\widehat{A}_2=\widehat{A}_1\)( gt ) nên \(\widehat{E}=\widehat{A}_2\Rightarrow\)tam giác CAE cân
Vậy AC = CE
Có AC > AB ( quan hệ giữa đường xiên và đường vuông góc )
Suy ra : CE > AB ( 1 )
Vẽ DF \(⊥\)AC , ta chứng minh được DF = DB
có DC > DF ( quan hệ giữa đường xiên và đường vuông góc ) suy ra : DC > DB
Ta có : DE2 = CE2 + DC2 ; AD2 = AB2 + DB2
Kết hợp ( 1 ) và ( 2 ) ta được : DE2 > AD2 . Do đó DE > AD ( 3 )
Từ ( 1 ), ( 2 ), ( 3 ) suy ra : CE + DC + DE > AB + DB + AD
hay chu vi tam giác ECD > chu vi tam giác ABD