Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6200mm3= 6,2ml= 6 200 000 000cm3= 6 200 000 000cc= 0.0062 l= 6,2x10-6m3
tk mik nha

Nửa chu vi hình chữ nhật là \(64:2=32\left(mm\right)\)
Chiều dài hình chữ nhật là: \(32\cdot\dfrac{3}{4}=24\left(mm\right)\)
Chiều rộng hình chữ nhật là:
32-24=8(mm)
Diện tích hình chữ nhật là:
\(24\cdot8=192\left(mm^2\right)\)


a, ke tia doi cua Ox la Ox'
=>goc x'Oy + yOx=180 ( 2 goc ke bu)
=>x'Oy = 180-120=60
ma OMm =60 (gt)
=> Oy//Mm ( dau hieu nhan bit 2 dt //)
b, co m'MO +OMm= 180 (ke bu)
=> m'MO = 180-60=120
ma Mt la pg OMm'
=> OMt= OMm'/2=120/2=60 (1)
* Ou la pg xOy => xOu= xOy/2=120/2=60
hay MOu =60 ( vi M thuoc Ox) (2)
1,2 => Ou // Mt ( DHNB2 dt //)
HINH THI CHIU KHO VE NHA

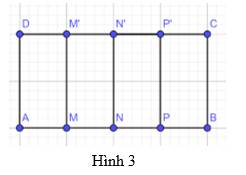
Đường trung trực của AB là NN’ vì NN' vuông góc với AB tại trung điểm N của AB.
Đường trung trực của AN là MM’ vì MM' vuông góc với AN tại trung điểm M của AN.
Đường trung trực của NB là PP’ vì PP' vuông góc với NB tại trung điểm P của NB.

Chắc là chứng minh \(\overline{M',N,D}\)
Lời giải:
Từ đkđb suy ra \(\frac{NC}{NM}=2,\frac{MM'}{MA}=\frac{1}{2}\)
Xét tam giác \(AMC\) ta có:
\(\frac{AD}{DC}.\frac{NC}{NM}.\frac{M'M}{MA}=1.2.\frac{1}{2}=1\)
Do đó theo định lý Menelaus ta có \(M',N,D\) thẳng hàng
Định lý Menelaus mình nhớ lớp 8 hay 9 gì đó có học.
Còn nếu không muốn sử dụng nó thì có thể dùng cách sau:
Ta thấy \(\frac{AM}{AM'}=\frac{AD}{AC}=\frac{1}{2}\) nên theo định lý Ta-lét đảo thì \(MD\parallel CM'\) và \(\frac{MD}{CM'}=\frac{1}{2}\)
Giả sử \(DM'\cap BC\equiv Q\)
Khi đó, do \(MD\parallel CM'\) nên dễ thấy \(\triangle DQM\sim M'QC\) theo trường hợp góc- góc
\(\Rightarrow \frac{DM}{M'C}=\frac{QM}{QC}=\frac{1}{2}\Rightarrow MQ=\frac{1}{3}MC\)
Do đó \(Q\equiv N\). Mà $Q,D,M'$ thẳng hàng nên $N,D,M'$ thẳng hàng
Ta có đpcm.